Please refer to Quadratic Equation Class 10 Mathematics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Mathematics books for Class 10. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 10 Mathematics Quadratic Equation Notes and Questions
Introduction to Quadratic Equations
Consider the equations
x2=36 ….(1)
x2+5x=6 ….(2)
In equation (1), variable occurs only in second degree. The quadratic equations involving a variable only in second degree is a Pure quadratic equation.
Thus, an equation that can be expressed in the form ax2+c=0, where a and c are real numbers and a ≠ 0 is a pure quadratic equation.
In equation (2) , variable occurs both in second and first degree. The quadratic equation involving a variable in both second and first degree is an Adfected quadratic equation.
Thus, an equation that can be expressed in the form ax2+bx+c=0, where a, b and c are real numbers and a ≠ 0 is an Adfected quadratic equation.
Now, let us learn about the roots of a quadratic equation.
Roots of a given quadratic equation are the values of the variables which satisfy that quadratic equation.
For example, consider the quadratic equation x2 – 8x + 15 = 0.
Here, L.H.S. = x2 – 8x + 15 and R.H.S. = 0
Let us substitute the different values of variable x in this equation and observe the results.
When x = 1 then x2 – 8x + 15 = 12 – 8(1) + 15 = 1 – 8 + 15 = 8 ∴ L.H.S. ≠ R.H.S.
When x = –1 then x2 – 8x + 15 = (–1)2 – 8(–1) + 15 = 1 + 8 + 15 = 24 ∴ L.H.S. ≠ R.H.S.
When x = 3 then x2 – 8x + 15 = 32 – 8(3) + 15 = 9 – 24 + 15 = 0 ∴ L.H.S. = R.H.S.
When x = 4 then x2 – 8x + 15 = 42 – 8(4) + 15 = 16 – 32 + 15 = –1 ∴ L.H.S. ≠ R.H.S.
When x = 5 then x2 – 8x + 15 = 52 – 8(5) + 15 = 25 – 40 + 15 = 0 ∴ L.H.S. = R.H.S.
When x = –5 then x2 – 8x + 15 = (–5)2 – 8(–5) + 15 = 25 + 40 + 15 = 80 ∴ L.H.S. ≠ R.H.S.
It can be observed that for x = 3 and x = 5, we have L.H.S. = R.H.S. which means that the equation x2 – 8x + 15 = 0 is satisfied. Thus, 3 and 5 are roots of this quadratic equation.
In other words, we can say that x = 3 and x = 5 are the solutions of quadratic equation x2 – 8x + 15 = 0.
Also, for x = 1, x = –1, x = 4 and x = –5, we have L.H.S. ≠ R.H.S. which means that the equation x2 – 8x + 15 = 0 is not satisfied. Thus, 1, –1, 4 and –5 are not the roots or solution of this quadratic equation.
Let us go through few examples to understand the concept better.
Example 1: Is the equation (x4)1/2+6 =0 a quadratic equation?
Solution:
The given equation is (x4)1/2+6 =0
We can also write it as
x4×1/2+6 =0
x2+6 =0
Hence, we can say that the given equation is a quadratic equation.
Example 2: Among the values given below find the roots of the quadratic equation 2x2 + 5x – 3 = 0.
x=1,x=1/2,x=2,x=-3,x=-3/4
Solution:
We have,
Equation: 2x2 + 5x – 3 = 0
Values: x = 1,x=1/2 , x = 2, x = –3,x=-3/4
Let us substitute the given values of x in the equation and observe the results.
When x = 1 then 2x2 + 5x – 3 = 2(1)2 + 5(1) – 3 = 2 + 5 – 3 = 4 ∴ L.H.S. ≠ R.H.S.

∴ L.H.S. = R.H.S.
When x = 2 then 2x2 + 5x – 3 = 2(2)2 + 5(2) – 3 = 8 + 10 – 3 = 15 ∴ L.H.S. ≠ R.H.S.
When x = –3 then 2x2 + 5x – 3 = 2(–3)2 + 5(–3) – 3 = 18 – 15 – 3 = 0 ∴ L.H.S. = R.H.S.
When x=-3/4 then

∴ L.H.S. ≠ R.H.S.
Only, x=1/2 and x = –3 satisfy the given quadratic equation.
Thus, 1/2 and –3 are the roots of the given quadratic equation.
Example 3: If one root of the quadratic equation 3x2 + 4x – p = 0 is 2323 then find the value of p.
Solution:
Since 2323 is a root of the equation 3x2 + 4x – p = 0, it must satisfy the equation.

Example 4: State whether m is a root of the equation 2x2 – (2m + 3)x + 3m = 0 or not.
Solution:
If m is a root of the equation 2x2 – (2m + 3)x + 3m = 0 then it would satisfy the equation.
Let us check it by substituting x = m in the given equation
2m2 – (2m + 3)m + 3m
= 2m2 – 2m2 – 3m + 3m
= 0
∴ L.H.S. = R.H.S.
Hence, m is a root of the equation 2x2 – (2m + 3)x + 3m = 0.
Expressing Given Situations as Quadratic Equations in One Variable
Quadratic equations arise in several situations around us and in different fields of mathematics. But how is a quadratic equation formulated?
Let us learn to express a situation mathematically.
Suppose there are two squares as shown in the following figure.

The sum of the areas of these two squares is 482 m2 and the difference of their perimeters is 32 m. Can we form a quadratic equation for the given mathematical situation?
Example1: An express train takes 1 hour less than a passenger train to travel a distance of 132 km. If the average speed of the express train is 11 km/h more than that of a passenger train, then form a quadratic equation to find the average speed of the express train?
Solution:
Let the average speed of the express train be x km/h.
Since it is given that the speed of the express train is 11 km/h more than that of a passenger train,
Therefore, the speed of the passenger train will be x −11 km/h.
Also we know that time= distance/speed
Time taken by the express train to cover 132 km = 132/x
Time taken by the passenger train to cover 132 km =132/x-11
And the express train takes 1 hour less than the passenger train. Therefore,

This is the required quadratic equation.
Example 2: A chess board contains 64 equal squares and the area of each square is 6.25 cm2. A border 2 cm wide is made around the board. Formulate a quadratic equation to find the length of each side of the board?
Solution:
Let the length of each side of the chess board be x cm.
Therefore, the length of the chess board without border will be x − 4 cm as shown in the following figure.

Area of the chess board without border = (x − 4)2
It is given that the area of each square is 6.25 cm2.
Area of 64 squares on the chess board = 6.25 × 64
Therefore,
(x − 4)2 = 64 × 6.25
x2-8x+16=400
x2-8x-384=0
This is the required quadratic equation.
Solution of Quadratic Equations by the Method of Factorization
Quadratic equations come from many real life situations. Let us consider one such situation.
The area of a rectangular garden is 500 m2 and its length is 5 m more than its breadth. Canwe find the length and breadth of the garden?
The garden can be drawn as
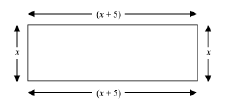
Let the breadth of the garden be x m.
Then, according to the given information, its length must be (x + 5) m.
Now, area of the garden = length × breadth = (x + 5) × x
The area of the garden is given as 500 m2.
∴ (x + 5) × x = 500
We can rewrite this equation as
x2 + 5x = 500
⇒ x2 + 5x – 500 = 0
This is a quadratic equation in variable x.
The length and the breadth of the garden can be calculated by solving the given quadratic equation.
How do we solve a quadratic equation? There are three methods of solving a quadratic
equation, one of which is the method of factorization.
We have now expressed the equation x2 + 5x – 500 = 0 as the product of two factors, (x + 25) and (x – 20). We can find the solutions of this equation by equating each factor to 0.
∴ x + 25 = 0 and x – 20 = 0
⇒ x = –25 and x = 20
However, the breadth of a park cannot be negative.
∴ x = 20
Thus, breadth of the park = 20 m and length of the park = (20 + 5) m = 25 m.
Let us now look at some more examples to get a grasp on this concept.
Example 1: Find the roots of the equation x2-x=12.
Solution:
First, we rearrange the given equation according to the standard format.
x2 – x = 12
⇒ x2 – x – 12 = 0
We need a pair of numbers whose product is –12 and whose sum is –1.
These numbers are 3 and –4.
We can now rewrite the equation as
x2 – x – 12 = 0
⇒ x2 + 3x – 4x – 12 = 0
⇒ x(x + 3) – 4(x + 3) = 0
⇒ (x – 4)(x + 3) = 0
The solutions of the given equation can now be determined by equating the two factors to 0.
∴ (x – 4) = 0 and (x + 3) = 0
⇒ x = 4 and x = –3
Thus, the two roots of the quadratic equation are 4 and –3.
Example 2: Find the roots of the equation 6x2+5x=4 .
Solution:
First, we rearrange the given equation according to the standard format.
6x2 + 5x – 4 = 0
Here, we need to find two such numbers whose product is 6 × (–4) = –24 and whose sum is 5.
The required numbers are 8 and –3.
Now, [8 × (–3) = –24 and 8 + (–3) = 5]
6x2 + 5x – 4 = 0
⇒ 6x2 + 8x –3x – 4 = 0
⇒ 2x(3x + 4) – 1(3x + 4) = 0
⇒ (2x – 1)(3x + 4) = 0
⇒ 2x – 1 = 0 and 3x + 4 = 0
x=1/2 and-4/3
Thus, the roots of the given equation are 1/2 and -4/3.
Example 3: Find two positive consecutive odd integers whose product is 99.
Solution:
Let the first integer be x.
The next odd integer will thus be x + 2.
∴ x(x + 2) = 99
x2 + 2x – 99 = 0
x2 + 11x – 9x – 99 = 0
x(x + 11) – 9(x + 11) = 0
(x – 9)(x + 11) = 0
x – 9 = 0 and x + 11 = 0
x = 9 and x = –11
However, we know that the two integers are positive.
∴ x = 9
Thus, the two integers are 9 and (9 + 2) = 11.
Example 4: The width of a rectangle is 16 feet less than 3 times its length. If the area of the rectangle is 35 ft2, then what are the dimensions of the rectangle?
Solution:
Here, the width of the rectangle has been expressed in terms of its length.
Hence, let us take the length of the rectangle to be x.
Thus, width of the rectangle = 3x – 16
The area of the rectangle is 35 ft2.
∴ 35 = x(3x –16)
35 = 3x2 – 16x
3x2 – 16x – 35 = 0
3x2 – 21x + 5x – 35 = 0
3x(x – 7) + 5(x – 7) = 0
(3x + 5)(x – 7) = 0
3x + 5 = 0 and x – 7 = 0
x=-5/3 and x=7
However, the length of a rectangle cannot be negative.
∴ x = 7
Thus, length of the rectangle is x = 7 ft and the width of the rectangle is 3x – 16 = (3 × 7 –16) ft = 5 ft
Example 5: Difference between the ages of a father and his son is 22 years. If the product of their ages is 555 then what are their ages?
Solution:
Let the age of the son be x years.
Then age of the father will be 22 + x years.
Since the product of their ages is 555, we have
x(22 + x) = 555
⇒ 22x + x2 = 555
⇒ x2 + 22x – 555 = 0
⇒ x2 + 37x – 15x – 555 = 0
⇒ x(x + 37) – 15(x + 37) = 0
⇒ (x + 37) (x – 15) = 0
⇒ (x + 37) = 0 or (x – 15) = 0
⇒ x = –37 or x = 15
Age cannot be negative, so we consider x = 15.
∴ Age of son = 15 years
∴ Age of father = (22 + 15) years = 37 years
Example 6: A bus takes 3 hours more than a train to travel a distance of 770 km. The speed of the train is more than that of bus by 15 km/hr. What are the average speeds of the bus and train?
Solution:
Let the average speed of the bus be x km/hr.
Then the average speed of the train will be (x + 15) km/hr.
Time taken by bus to cover 770 km = Distance/Spees=770/x hours
Time taken by train to cover 770 km = Distance/Spees=770/x+15 hours
According to the question, we have
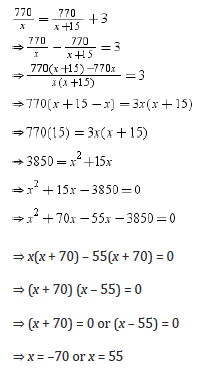
Speed cannot be negative, so we will consider x = 55.
∴ Average speed of bus = 55 km/hr
∴ Average speed of train = (55 + 15) km/hr = 70 km/hr
Solution of Quadratic Equations by Completing Squares
Many real life situations can result in quadratic equations.
For example, consider the following situation:
A ladder is leaning against a wall. The top of the ladder touches the wall at a height of 15 feet. The length of the ladder is one foot more than twice its distance from the foot of the wall. We need to find the length of the ladder.
We can express the given situation mathematically with the help of a quadratic equation.
Let us see how.
Let the distance from the wall to the bottom of the ladder be x feet.
It is given that the length of the ladder is one foot more than twice its distance from the foot of the wall.
Hence, the length of the ladder becomes (2x + 1).
The wall makes an angle of 90° with respect to the ground. Since the ladder is leaning against the wall, the entire arrangement forms a right triangle in which the ladder acts as the hypotenuse.
On applying Pythagoras theorem, we get

Now, to find the length of the ladder, we first need to solve the given quadratic equation.Observe that if you try to solve it by splitting the middle term, then it will become very lengthy. In such cases, it is easier to solve the quadratic equation by another method called the Completion of Squares.
Let us learn this method with the help of an example.
Consider the following quadratic equation:
x2-6x-7=0
In this method, we need to convert the quadratic equation in the form
(x-p)2-q2=0
To convert a quadratic equation in this form, we will make use of the following identities:

In the example taken previously, the given equation was x2-6x-7=0.
Note that the term with the coefficient x has a negative sign attached to it.
We thus need to make use of the identity (x-b)2=x2-2xb+b2 here.
On comparing this equation with the given identity, we get 2b = 6, i.e., b = 3.
Thus, we need to add b2=32=9 on both sides of the equation.
The equation now becomes x2-6x-7+9=0+9.

It is important to remember that √16 has two values, i.e., 4 and –4.
Thus, the equation can be further simplified as
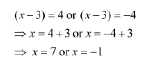
Thus, the given equation has two solutions, i.e., x = 7 and x = –1.
Let us now go back to the initial problem we were discussing.
We had arrived at a final quadratic equation, which was 3x2+4x-224=0 .
Note that in this case, the term with the coefficient x2 is not a perfect square. We thus need to multiply the equation by 3 to make it a perfect square.
On doing so, we get

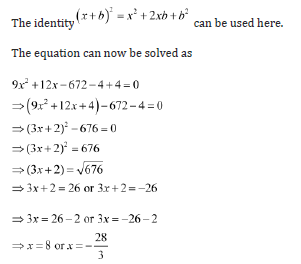
However, x represents the distance of the foot of the ladder from the base of the wall, which cannot be negative. Thus, x has only one value, i.e., 8.
Thus, length of the ladder = 2x + 1 = (2 × 8 + 1) ft = 17 ft
We can follow one more approach to solve this equation.
The equation was 3x2+4x-224=0.
Here, the term with the coefficient x2 is not a perfect square. We thus convert it to a perfect square by multiplying the equation by 3.
Note that we could also have divided the equation by 3 and still have converted the term to a perfect square.
Let us see how.


We can use any of the two methods mentioned above, as long as we covert the equation to the form (x-p)2-q2=0
Note: Usually, the roots of the quadratic equation ax2+bx+c=0 ,where a≠0 can be found by first dividing the equation by a and then completing the squares of the terms in the equation.
Example 1: Find the roots of the equation 5x2-6x+1=0 by the method of completion of squares.
The given equation is 5x2-6x+1=0 .
By multiplying the equation by 5, we get 25x2-30x+5=0
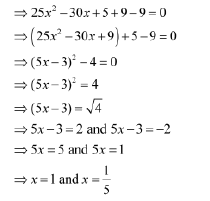
Example 2: Find the roots of the equation x2+x+1=0by the method of completion of squares.
Solution:

Example 3: Find three consecutive even integers so that the product of the first two numbers is three times the third number.
Solution:
Let the three numbers be x, (x + 2), and (x + 4).
From the given condition, we have x(x + 2) = 3(x + 4).

However, the three numbers are positive integers.
Thus, x cannot be equal to –3.
Thus, the three consecutive even integers are 4, 6, and 8.
Example 4: Denominator of a fraction is 3 more than its numerator such that both are positive integers. If the sum of the fraction and its reciprocal is then find the fraction.
Solution:
Let the numerator be x. Then the denominator will be x + 3.
According to the question, we have


Example 5: Base of a small triangular garden is 7 m more than its height. If the area of the garden is 60 m2 then find its base and height.
Solution:
Let the height of the triangular garden be x m. Then its base will be (x + 7) m.
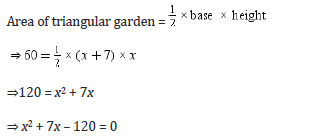

Length cannot be negative, so we consider x = 8.
∴ Height of triangular garden = 8 m
∴ Base of triangular garden = (8 + 7) m = 15 m
Solution of Quadratic Equations by Using Quadratic Formula
The following equations are quadratic in nature:

If we were to solve these equations, we could have either factorized the equations (i), (ii), and (iii) or completed their squares.
However, note that we would face a lot of difficulty in solving equation (iv) by either of these two methods.
Apart from factorizing a quadratic equation or completing its square, we can also use the quadratic formula to factorize an equation.
Let us go back to equation (iv), which was 2√6x2 -2√13x+√6=0.
Comparing this equation with the general form of a quadratic equation:

Let us now solve some more quadratic equations by using the quadratic formula.
Example 1: Solve the quadratic equation 5x2 + x− 22 = 0 by using the quadratic formula.
Solution:
On comparing the given equation with the general form ax2 + bx + c = 0, we get
a = 5, b = 1, c = −22
On putting these values in the quadratic formula, we get

Example 2: Find the roots of the equation 3x2 + 5x + 10 = 0 by using the quadratic equation formula.
Solution:
On comparing the given equation with the general form ax2 + bx + c = 0, we get
a = 3, b = 5, c = 10
∴ b2 − 4ac = (5)2 − 4 × 3 × 10
= 25 − 120
= −95 <</span> 0

Thus, there are no real roots for the given equation.
Example 3: The denominator of a fraction is 2. If the sum of the fraction and its reciprocal is 13/6 , then find the fraction.
Solution:
Let the numerator of the fraction be x.

On comparing this equation with the general form ax2 + bx + c = 0, we get
a = 6, b = −26, c = 24
On putting these values in the quadratic formula, we get

Since x is the numerator of the fraction, it has to be an integer.
∴ x = 3
Thus, the fraction is x/2= 3/2 .
Example 4: The perimeter of a rectangle is 34 cm and its area is 70 cm2. Find the length and the breadth of the rectangle.
Solution:
Let the length and breadth of the rectangle be x and y respectively.
Thus, perimeter of the rectangle = 2(x + y) = 34 cm
⇒ x + y = 17
⇒ y = 17 – x … (1)
Thus, area of the rectangle = x × y = 70 cm2 … (2)
Substituting the value of y from (1) in (2):
x(17 – x) = 70
⇒ 17x – x2 = 70
⇒ x2 – 17x + 70 = 0
By using the quadratic formula, we get
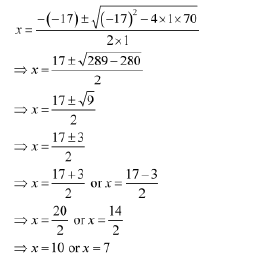
Thus, the length and the breadth of the rectangle are 10 cm and 7 cm respectively.
Example 5: A ball is thrown upwards from a height of 6 m with a particular speed.The height h of the ball after t seconds is given by 6 + 13t – 5t2. How long the ball will take to touch the ground?
Solution:
Height of the ball after t seconds is given as follows:
h = 6 + 13t – 5t2
When ball will touch the ground, the height will be 0 m.
⇒ 0 = 6 + 13t – 5t2
⇒ 5t2 – 13t – 6 = 0
By using the quadratic formula, we get

Time cannot be negative, so we will consider t = 3.
Thus, the ball will touch the ground after 3 seconds.
Example 6: A super fast train takes 6 hours less than a passenger train to reach the destination which is 1440 km away. If the speed of the super fast train is 40 km/hr more than that of passenger train then find the average speed of both trains.
Solution:
Let the average speed of passenger train be x km/hr.
Then the average speed of super fast train will be x + 40 km/hr.
Total distance to be covered = 1440 km


Speed cannot be negative, so we consider x = 80.
∴ Average speed of passenger train = 80 km/hr
∴ Average speed of super fast train = (80 + 40) km/hr = 120 km/hr
Conditions Under which a Quadratic Equation has Real or Imaginary Roots
A right angled ΔABC is given in the following figure.
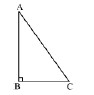
In this triangle, the base BC is 5 cm less than twice its height AB. The hypotenuse of the triangle is 2 cm.
Is the above given situation possible for triangle ΔABC?
Can we also find the nature of roots of a quadratic equation without solving the equation?
We can see from the above example that the value of x depends on the value under the sign of square root. If this value is positive, then the value of x will be real and if it is
negative, the value of x will be imaginary.
Thus, we can say that the nature of the values of x in quadratic equation ax2 + bx + c = 0,depends on the value of b2 − 4ac.
Here, b2 − 4ac is called the discriminant of the quadratic equation ax2 + bx + c = 0.
The value of b2 − 4ac determines the nature of the roots of a quadratic equation.
A quadratic equation ax2 + bx + c = 0 has
(i) Two distinct real roots, if b2 − 4ac > 0 or b2 > 4ac
(ii) Two equal real roots, if b2 − 4ac = 0 or b2 = 4ac
(iii) No real roots or imaginary roots if b2 − 4ac < 0 or b2 < 4ac
For example: The quadratic equation 3x2 − x + 2 = 0 has no real root because for this equation,b2 − 4ac = (−1)2 − 4 × 3 × 2
= 1 − 24
= − 23 < 0
Here b2 − 4ac < 0.
Thus, the equation 3x2 − x + 2 = 0 has no real roots.
Now, let us solve some more examples based on the natures of roots of quadratic equations.
Example 1: Find the value of discriminant for the quadratic equation x2 + 4x − 21 = 0.
Solution:
The given quadratic equation is x2 + 4x − 21 = 0.
On comparing this equation with the standard form of quadratic equation, ax2 + bx + c = 0,
we have
a = 1, b = 4, c = − 21
Therefore, the discriminant, b2 − 4ac = (4)2 − 4 × 1 × (− 21)
= 16 + 84
= 100
Thus, the value of discriminant for the given quadratic equation is 100.
Example 2: Find the nature of the roots of quadratic equation, x2 − 8x + 16 = 0.
Solution:
The given equation is x2 − 8x + 16 = 0.
On comparing this equation with the standard form of quadratic equation, ax2 + bx + c = 0,
we have a = 1, b = − 8, c = 16.
Therefore, the discriminant,
b2 − 4ac = (− 8)2 − 4 × 1 × 16
⇒ b2 − 4ac = 64 − 64
⇒ b2 − 4ac = 0
Thus, the given quadratic equation has two equal real roots.
Example 3: Find the value of k for which the quadratic equation x2 − 12x + k = 0 has two real equal roots.
Solution:
On comparing the given equation with ax2 + bx + c = 0, we have a = 1, b = − 12, c = k
For two real equal roots,
b2 − 4ac = 0
⇒ (− 12)2 − 4 × 1 × k = 0
⇒ 144 − 4k = 0
⇒ 4k = 144
⇒ k = 36
Thus, the value of k is 36.
Example 4: Is it possible to design a rectangular garden whose area is 250 square m and the sum of whose length and breadth is 20 m?
Solution:
Let the length of the garden be x m.
∴ Breadth = (20 − x) m
Area of garden = length × breadth
250 = x × (20 − x)
250 = 20x − x2
⇒ x2 − 20x + 250 = 0
This is a quadratic equation whose discriminant is b2 − 4ac = (− 20)2 − 4 × 1 × 250
= 400 − 1000
= − 600 < 0
Therefore, the roots of the equation are not real. Hence, it is not possible to design such a garden.
Example 5: Can we find two consecutive positive numbers whose product is 420? If yes, then find the numbers.
Solution:
Let one number be x.
Then the other number = x + 1
According to the question,
x × (x + 1) = 420
⇒ x2 + x = 420
⇒ x2 + x − 420 = 0
The discriminant of this equation is b2 − 4ac = (1)2 − 4 × 1 × (− 420)
= 1 + 1680
= 1681
∴ b2 − 4ac > 0
Therefore, the roots of the quadratic equation x2 + x − 420 = 0 are real.
We can find the numbers using quadratic formula as follows

x = 20 and − 21
We take x = 20, as − 21 is a negative number.
Thus, 20 and 21 are the two consecutive positive numbers whose product is 420.

We hope the above Quadratic Equation Class 10 Mathematics are useful for you. If you have any questions then post them in the comments section below. Our teachers will provide you an answer. Also refer to MCQ Questions for Class 10 Mathematics


