Students can read the important questions given below for Differential Equations Class 12 Mathematics. All Differential Equations Class 12 Notes and questions with solutions have been prepared based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS. You should read all notes provided by us and Class 12 Mathematics Important Questions provided for all chapters to get better marks in examinations. Mathematics Question Bank Class 12 is available on our website for free download in PDF.
Important Questions of Differential Equations Class 12
Very Short Answer Type Questions
Question. Find order and degree of differential equation
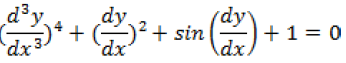
Answer. Order=3
Degree not defined
Question. Find order and degree of differential equation
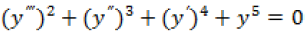
Answer. Order=3
Degree=2
Question. Integrating factor of
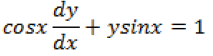
Answer.
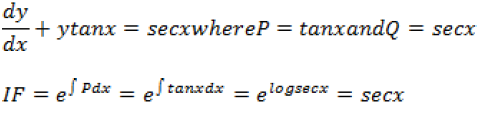
Question. For what value of n is the following a homogeneous differential equation:
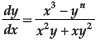
Answer. 3
Question. Form the differential equation not containing the arbitrary constants and satisfied by the equation: y = peqx.
Answer.
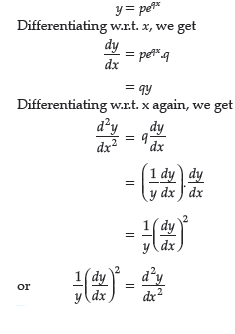
Question. Write the order and the degree of the following differential equation:
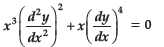
Answer. Order = 2, degree = 2
Question. Find the differential equation of the family of lines passing through the origin.
Answer. Generates equation of family of lines passing through origin
y = mx ⇒ m = y/x
dy/dx = m = slope
dy/dx = y/x
x dy/dx – y = 0
Question. Find the solution of the differential equation dy/dx = x3e-2y
Answer.
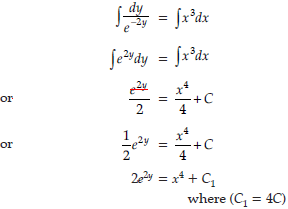
Question. How many arbitrary constants are there in the particular solution of the differential equation
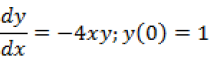
Answer. 0
Question. For what value of n is the following a homogeneous differential equation:
Answer. 3
Short Answer Type Questions
Question. Solve the differential equation
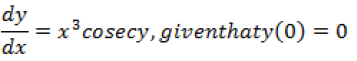
Answer.
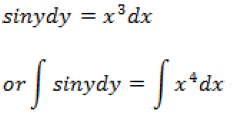
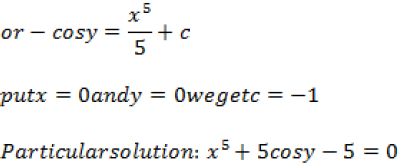
Question. Solve the differential equation
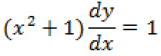
Answer.
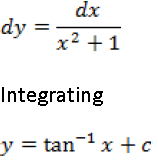
Question. Form the differential equation of all circles which is touching the x-axis at the origin.
Answer. (x – 0)2 + (y – r)2 = r2
x2 + y2 = 2ry
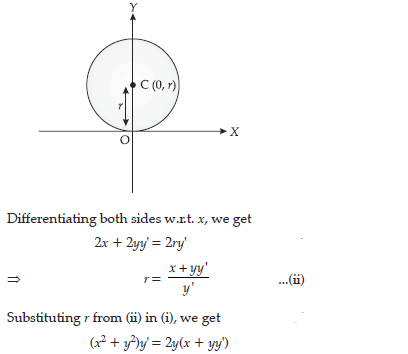
Question. Form the differential equation representing the family of curves y = aebx+5, where ‘a’ and ‘b’ are arbitrary constants
Answer.
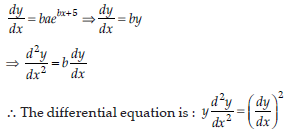
Question. Find the general solution of the differential equation:
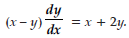
Answer. Given differential equation can be written as
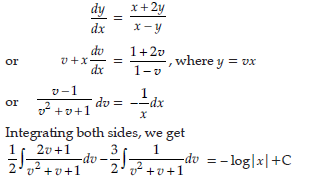

Question. Prove that x2 – y2 = C(x2 + y2)2 is the general solution of the differential equation (x2 – 3xy2) dx = (y3 – 3x2y) dy, where C is a parameter
Answer. x2 – y2 = C(x2 + y2)2
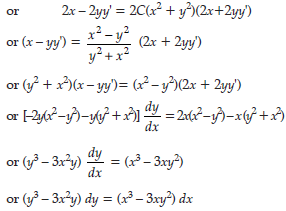
Hence x2 – y2 = C(x2 + y2)2 is the solution of given differential equation.
Question. Solve the following differential equation: dy/dx = x3 cosec y, given that y(0) = 0.
Answer.
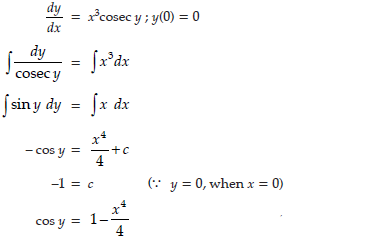
Question. Find the general solution of the differential equation.
xy dy/dx = dy/dx = (x+2)(y+2)
Answer.
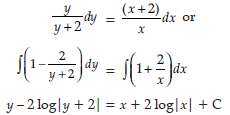
Question. Find the general solution of the differential equation dy/dx + 2/x y = x
Answer. Integrating factor is
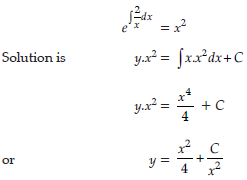
Question. Find the integrating factor of the differential equation dy/dx +y = 1+y/x
Answer. Given differential equation can be written as
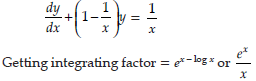
Question. Find the differential equation of the family of curves y = Ae2x + Be–2x, where A and B are arbitrary constants.
Answer. Differentiating y = Ae2x + Be–2x, we get
dy/dx = 2Ae2x + 2Be–2x
differentiate again to get
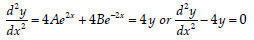
Question. Can y = ax + b/a be a solution of the following differential equation ?
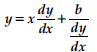
If no, find the solution of the D.E.
Answer.
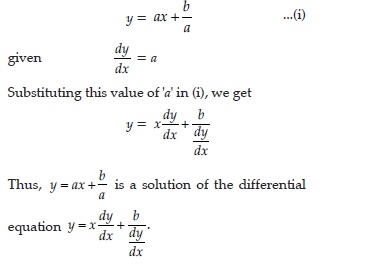
Question. Find the equation of curve whose tangent at any point on it, different from origin, has slope
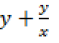
Answer.
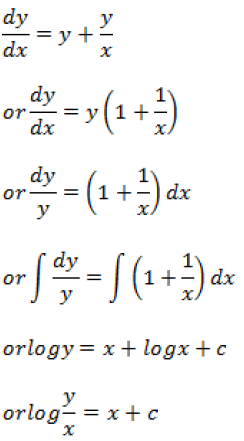
Question. Solve the differential equation
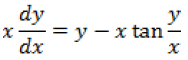
Answer.
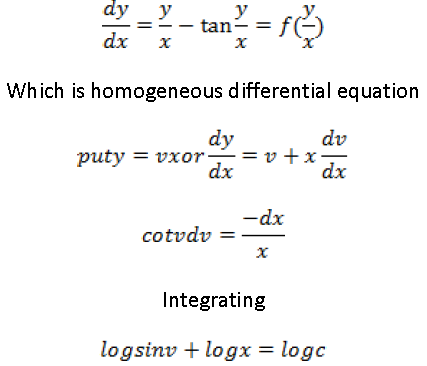
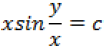
Question. Solve the differential equation
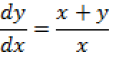
Answer.
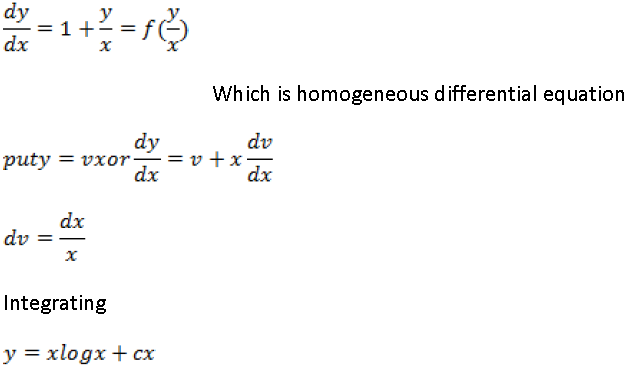
Question. Solve the differential equation
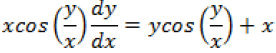
Answer.

Question. Solve the differential equation
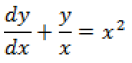
Answer.
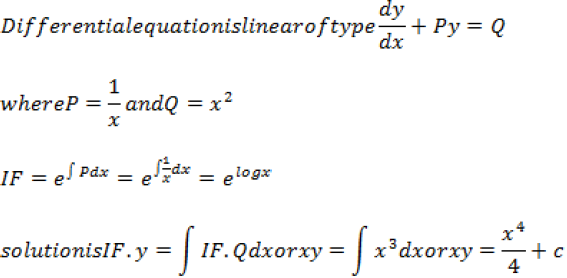
Question. Show that the differential equation
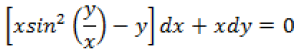
Is homogeneous.
Find the particular solution given that y = π/4 when x = 1
Answer.
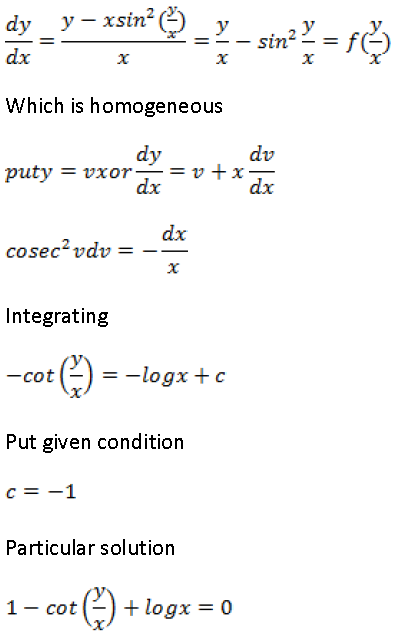
Question. Find the general solution of the differential equation
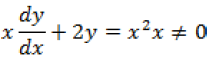
Answer.
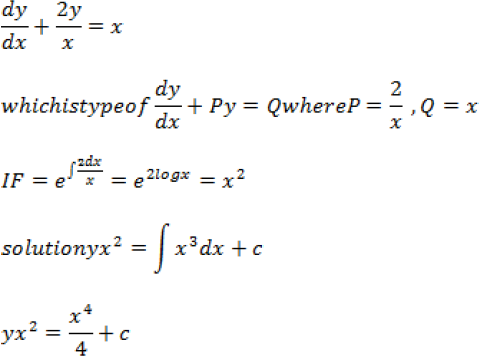
Question. For the differential equation
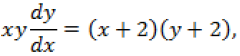
Find the solution curve passing through the point (1, -1)
Answer.
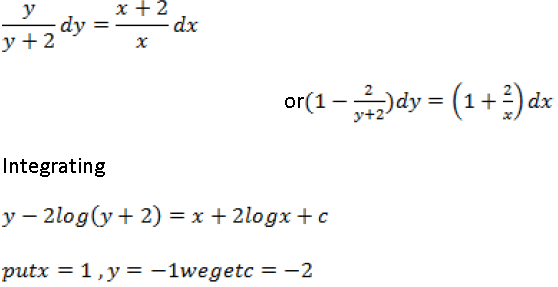
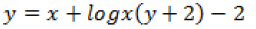
Long Answer Type Questions:
Question. Solve the differential equation:
dy/dx – 3y cot x = sin 2x given y = 2, when x= π/2
Answer.
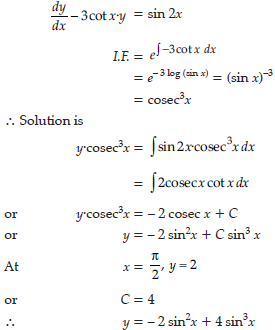
Question. Solve: (1 + x2 + y2 + x2y2)dx + xydy = 0, given that y = 0 and x = 1.
Answer. The given equation can be written as:
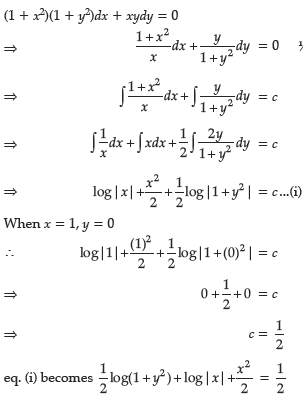
Question. Find the particular solution of the differential equation:
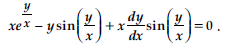
for x = 1, y = 0.
Answer. Given differential equation is homogeneous.
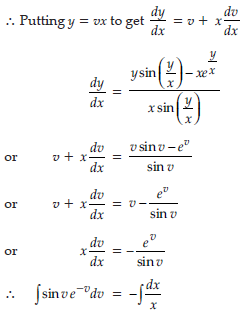
Question. Show that the differential equation
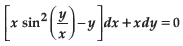
is homogeneous. Find the particular solution of this differential equation, given that y = π/4 when x = 1.
Answer.
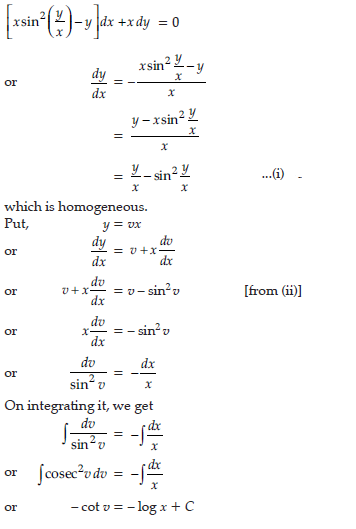
Question. Solve the differential equation x2dy + (xy + y2) dx = 0 given y = 1, when x = 1.
Answer. x2dy + (xy + y2) dx = 0
CASE STUDY :
Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation 𝒅𝒚/𝒅𝒙=𝐤(𝟓𝟎−𝐲) where x denotes the number of weeks and y the number of children who have been given the drops.
Question. State the order of the above given differential equation.
Answer : Order is 1
Question. Which method of solving a differential equation can be used to solve 𝒅𝒚/𝒅𝒙=𝐤(𝟓𝟎−𝐲).?
a. Variable separable method
b. Solving Homogeneous differential equation
c. Solving Linear differential equation
d. all of the above
Answer
A
Question. The solution of the differential equation 𝒅𝒚/𝒅𝒙=𝐤(𝟓𝟎−𝐲) is given by,
a. log | 50 – y| = kx + C
b. – log | 50 – y| = kx + C
c. log | 50 – y| = log| kx |+ C
d. 50 – y = kx + C
Answer
B
Question. The value of c in the particular solution given that y(0)=0 and k = 0.049 is.
a. log 50
b. log 1/50
c. 50
d. -50
Answer
B
Question. Which of the following solutions may be used to find the number of children who have been given the polio drops?
a. y = 50 – ekx
b. y = 50 – e=kx
c. y = 50 ( 1 – e-kx)
d. y = 50 ( e=kx – 1)
Answer
C

