Please refer to Gravitation Class 11 Physics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Physics books for Class 11. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 11 Physics Gravitation Notes and Questions
CONCEPTS
• Kepler’s law of planetry motion
(a) Kepler’s first law (law of orbit): Every planet revolves around the sun in an elliptical orbit with the sun is situated at one focus of the ellipse.
(b) Kepler’s second law (law of area): The radius vector drawn from the sun to a planet sweeps out equal areas in equal intervals of time , i.e., the areal velocity of the planet around the sun is constant.
(c) Kepler’s third law (law of period): The square of the time period of revolution of a planet around the sun is directly proportional to the cube of semimajor axis of the elliptical orbit of the planet around the sun.
• Gravitation is the name given to the force of attraction acting between any two bodies of the universe.
• Newton’s law of gravitation: It states that gravitational force of attraction acting between two point mass bodies of the universe is directly proportional to the product of their masses and is inversely proportional to the square of the distance between them, i.e., F=Gm1m2/r2, where G is the universal gravitational constant.
• Gravitational constant (G): It is equal to the force of attraction acting between two bodies each of unit mass, whose centres are placed unit distance apart. Value of G is constant throughout the universe. It is a scalar quantity. The dimensional formula G =[M-1L3T-2]. In SI unit, the value of G =6.67X10- 11Nm2kg-2.
Gravity: It is the force of attraction exerted by earth towards its centre on a body lying on or near the surface of earth. Gravity is the measure of weight of the body. The weight of a body of mass m=mass X acceleration due to gravity=mg. The unit of weight of a body will be the same as those of force.
• Acceleration due to gravity (g): It is defined as the acceleration set up in a body while falling freely under the effect of gravity alone. It is vector quantity.The value of g changes with height, depth, rotation of earth the value of g is zero at the centre of the earth. The value of g on the surface of earth is 9.8 ms-2 . The acceleration due to gravity (g) is related with gravitational constant (G) by the relaion, g=GM/R2 where M and R are the mass and radius of the earth.
• Variation of acceleration due to gravity:
(a) Effect of altitude, g’=Gr2/(R+h)2 and g’=g(1-2h/R)
The first is valid when h is comparable with R and the second relation is valid when h<<R.
The value of g decreases with increase in h.
(b) Effect of depth g’=g(1-d/R)
The acceleration due to gravity decreases with increase in depth d and becomes zero at the center of earth.
(c) Effect of rotation of earth: g’=g-R ω2cos2λ
The acceleration due to gravity on equator decreases on account of rotation of earth and increase with the increase in latitude of a place.
• Gravitational field: It is the space around a material body in which its gravitational pull can be experienced by other bodies. The strength of gravitational field at a point is the measure of gravitational intensity at that point. The intensity of gravitational field of a body at a point in the field is defined as the force experienced by a body of unit mass placed at that point provided the presence of unit mass does not disturb the original gravitational field. The intensity of gravitational field at a point distance r from the center of the body of mass M is given by E=GM/r2=acceleration due to gravity.
• Gravitational potential: The gravitational potential at a point in a gravitational field is defined as the amount of work done in bringing a body of unit mass from infinity to that point without acceleration. Gravitational potential at a point, V=work
done(W)/test mass(m0)= -GM/r. V= W/mo = – GM / r
Gravitational intensity (I) is related to gravitational potential (V) at a point by the relation, E= -dV/dr
• Gravitational potential energy of a body, at a point in the gravitational field of another body is defined as theamount of work done in bringing the given body from infinity to that point without acceleration.
Gravitational potential energy U=gravitational potential X mass of body =-GM / r Xm.
• Inertial mass of a body is defined as the force required to produce unit acceleration in the body.
Gravitational mass of a body is defined as the gravitational pull experienced by the body in a gravitational field of unit intensity.
Inertial mass of a body is identical to the gravitational
mass of that body. The main difference is that the gravitational mass of a body is affected by the presence of other bodies near it. Whereas the inertial mass of a body remains unaffected by the presence of other bodies near it.
• Satellite: A satellite is a body which is revolving continuously in an orbit around a comparatively much larger body.
(a) Orbital speed of satellite is the speed required to put the satellite into given orbit around earth.
• Time period of satellite(T): It is the time taken by satellite to complete one revolution around the earth.
T= 2π /R √(R + h)3/g
• Height of satellite above the earth surface:
h=(T2R2g/4π2)1/3 – R
• Total energy of satellite, E=P.E +K.E=GM–/2(R+h)
Blinding energy of satellite = -E = GM m/(R+h)
• Geostationary satellite: A satellite which revolves around the earth with the same angular speed in the same direction as is done by the earth around its axis is called geostationary or geosynchronous satellite. The height of geostationary satellite is = 36000 km and its orbital velocity = 3.1 km s-1.
• Polar satellite: It is that satellite which revolves in polar orbit around earth ,i.e. , polar satellite passes through geographical north and south poles of earth once per orbit.
• Escape speed: The escape speed on earth is defined as the minimum speed with which a body has to be projected vertically upwards from the surface of earth( or any other planet ) so that it just crosses the gravitational field of earth (or of that planet) and never returns on its own. Escape velocity ve is
given by, ve =√2GM/R = √2gR . For earth, the value of escape speed is 11.2kms-1.
• For a point close to the earth’s surface , the escape speed and orbital speed are related as ve =√2vo
• Weightlessness: It is a situation in which the effective weight of the body becomes zero.

Question and Answer :
Question. According to Kepler’s second law the radius vector to a planet from the sun sweeps out equal area in equal interval of time. The law is a consequence of which conservation law.
Answer. Law of Conservation of angular momentum.
Question.What are the factors which determine ; Why some bodies in solar system have atmosphere and others don’t have?
Answer. The ability of a body (planet) to hold the atmosphere depends on acceleration due to gravity.
Question. What is the maximum value of gravitational potential energy and where?
Answer. The value of gravitational potential energy is negative and it increases as we move away from the earth and becomes maximum ( zero) at infinity.
Question.The gravitational potential energy of a body at a distance r from the center of earth is U. What is the weight of the body at that point?
Answer. U=

Question.When a stone of mass m is falling on the earth of mass M; find the acceleration of earth if any?
Answer. Force exerted by falling stone on earth, F=mg
Acceleration of earth= F/M = mg/M
Question. Why G is called a universal constant?
Answer. It is so because the value of G is same for all the pairs of the bodies (big or small) situated anywhere in the universe.
Question. A satellite revolving around earth loses height. How will its time period be changed?
Answer. Time period of satellite is given by;T=2π √(R+h)3/GM. Therefore ,T will decrease, when h decreases.
Question. Should the speed of two artificial satellites of the earth having different masses but the same orbital radius, be the same?
Answer. Yes it is so because the orbital speed of a satellite is independent of the mass of a satellite. Therefore the speeds of the artificial satellite will be of different masses but of the same orbital radius will be the same.
Question. Can a pendulum vibrate in an artificial satellite?
Answer. No, this is because inside the satellite, there is no gravity ,i.e., g=0.
As t = 2π√l /g , hence, for g=0 , t = ∞. Thus, the pendulum will not vibrate.
Question. Why do different planets have different escape speed?
Answer. As, escape speed =√2GM /R , therefore its value are different for different planets which are of different masses and different sizes.
Question. Show that weight of all body is zero at Centre of earth?
Answer. The value of acceleration due to gravity at a depth d below the surface of earth of radius R is given by ɠ=g(1-d/R).At the center of earth, (dept)d=R; so, ɠ =0.The weight of a body of mass m at the centre of earth =mg’=m x 0=0.
Question. If a person goes to a height equal to radius of the earth from its surface. What would be his weight relative to that on the earth.
Answer. At the surface of the earth, weight W=mg=GM m/R2.
At height h =R , weight W’=mg’=GMm/(R +h )z = GM m/(R+h)z W,/W =Rz/(2R)z = 1/4 W’ = w/4
It means the weight would reduce to one-fourth of the weight on the surface of earth.
Question. What will be the effect on the time period of a simple pendulum on taking to a mountain?
Answer. The time period of a pendulum, T=2π√l /g, i.e., T= 1/√g .As the value of g is less at mountain than at plane, hence time period of simple pendulum will be more at mountain than at plane though the change will be very small.
Question. A satellite is revolving around the earth, close to the surface of earth with a kinetic energy E. How much kinetic energy should be given to it so that it escapes from the surface of earth?
Answer. Let voce be the orbital and escape speeds of the satellite, then va =√2va;
Energy in the given orbit , E1 =1/2 mv2/o = E
Energy for the escape speed, E2 = 1/2 mv2/e =1/2m(√2v2/o) = 2E
Energy required to be supplied = E2 – E1 = E .
Question. Draw graphs showing the variation of acceleration due to gravity with (a)height above the earth’s surface, (b)depth below the Earth’s surface.
Answer. (a)The variation of g with height h is related by relation g 1/ where r=R+h.
Thus, the variation of g and r is a parabolic curve.
(b)The variation of g with depth is released by equation g’=g(1-d/R) i.e. g’ ∝ (R-D )
.Thus, the variation of g and d is a straight line.
Question. Why does moon have no atmosphere?
Answer. Moon has no atmosphere because the value of acceleration due to gravity ‘g’ on surface of moon is small. Therefore, the value of escape speed on the surface of moon is small. The molecules of atmospheric gases on the surface of the moon have thermal speeds greater than the escape speed. That is why all the molecules of gases have escaped and there is no atmosphere on moon.
Question. A rocket is fired with a speed v=2√gR near the earth’s surface and directed upwards. Find its speed in interstellar space.
Answer. Let v be the speed of rocket instellar space.

Question. A tennis ball and a cricket ball are to be projected out of gravitational field of the earth. Do we need different velocities to achieve so?
Answer. We require the same velocity for the two balls, while projecting them out of the gravitational field. It is so because, the value of escape velocity does not depend upon the mass of the body to be projected [i.e. ,va = √2gR].
Question. Suppose the gravitational force varies inversely as the nth power of the distance.
Show that the time period of a planet in circular orbit of radius R around the sun will be proportional to R(n+1)/2
Answer .


Question. A mass M is broken into two parts of masses m1 and m2. How are m1 and m2 related so that force of gravitational attraction between the two parts is maximum.
Answer . Let m1 = m ,then m2 = M – m. Gravitational force of attraction between them when placed distance r apart will be = Gm(M – m)/r2 .
Differentiating it w.r.t. m, we get
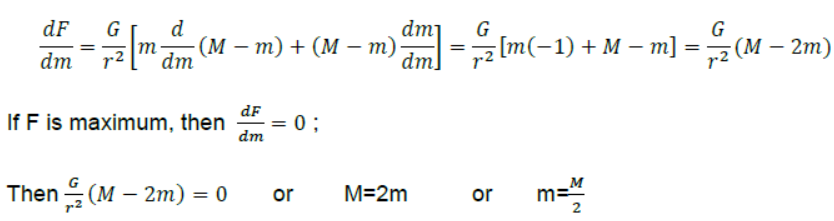
Question. Two particles of equal mass move in a circle of radius r under the action of their mutual gravitational attraction. Find the speed of each particle if its mass is m.
Answer . The two particles will move on a circular path if they always remain dramatically opposite so that the gravitation force on one particle due to other is directed along the radius. Taking into consideration the circulation of one particle we have
mv2 = Gmm/(2r)2 Or V = √Gm/4r
Question. The magnitude of gravitational field at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M are l1 and l2 respectively. Find the ratio of (l1 / l2) if r1 > R and r2 < R
Answer . When r1 > R, Ans. When the point lies outside the sphere . Then sphere can be considered to be a point mass body whose whole mass can be supposed to be concentrated at its Centre. Then gravitational intensity at a point distance r1 from the Centre of the sphere will be , l1 = GM /r12
When r2<R , the point P lies inside the sphere. The unit mass body placed at P, will experience gravitational pull due to sphere of radius r2 whose mass is M’= M 4/3πr23/4/3πR3 =Mr23/R3 .
Therefore, the gravitational intensity at P will be ,

Question. What are the conditions under which a rocket fired from earth, launches an artificial satellite of earth?
Answer. Following are the basic conditions:
(i) The rocket must take the satellite to a suitable height above the surface of earth for ease of propulsion.
(ii)From the desired height, the satellite must be projected with a suitable speed, called orbital speed.
(iii) In the orbital path of satellite, the air resistance should be negligible so that its speed does not decrease and it does not burn due to the heat produced.
Question. Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
Answer . The particles will always remain diametrically opposite so that the force on each particle will be directed along the radius. Consider the motion of one of the particles. The force on the particle is F = Gm2/4R2. If the speed is v, its acceleration is V2 /R
Thus by Newton’s Law,
Gm2/4R2 = mv2/R
V = √Gm/4R
Question. Two bodies of masses m1 and m2 are initially at rest at infinite distance apart.
They are then allowed to move towards each other under mutual gravitational attraction. Find their relative velocity of approach at a separation distance r between them.
Answer . Let vr be the relative velocity of approach of two bodies at a distance r apart.
The reduced mass of the system of two particles is , μ = m1 m2/m1 +m2
According to law of conservation of mechanical energy.
Decrease in potential energy = increase in K.E.

Question. Since the moon is gravitationally attracted to the earth, why does it not simply crash on earth?
Answer . The moon is orbiting around the earth in a certain orbit with a certain period . The centripetal force required for the orbital motion is provided to the gravitational pull of earth. The moon can crash into the earth if its tangential velocity is reduced to zero. AS moon has tangential velocity while orbiting around earth, it simply falls around the earth rather than into it and hence cannot crash into the earth.
Question. A particle is fired vertically upward with a speed of 3.8km/s. Find the maximum height attained by the particle. Radius of earth=6400km and g at the surface=9.8m/s. Consider only earth’s gravitation.
Answer . At the surface of the earth, the potential energy of the earth-particle system is GMm/R with usual symbol. The kinetic energy is 1/2 mv2 where vo = 9.8km / s. At the
maximum height the kinetic energy is zero. If the maximum height reached is H, the potential energy of the earth-particle system at this instant is – GMm/R +H . Using conservation of energy , – GMm/R + 1mv2 /2 = -GMm/R+H
Writing GM=gR2anddividing by m,

Question. A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
Answer . Let d be the distance from centre of earth to man ‘m’ then


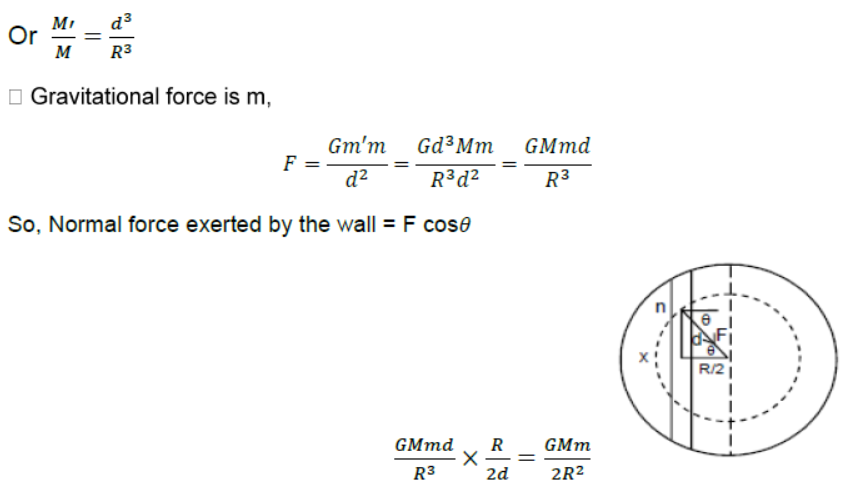
Question. (a) Find the radius of the circular orbit of a satellite moving with an angular speed equal to the angular speed of earth’s rotation.
(b) If the satellite is directly above the north pole at some instant , find the time it takes to come over equatorial plane. Mass of the earth= 6×1024kg
Answer . (a) Angular speed f earth & the satellite will be same
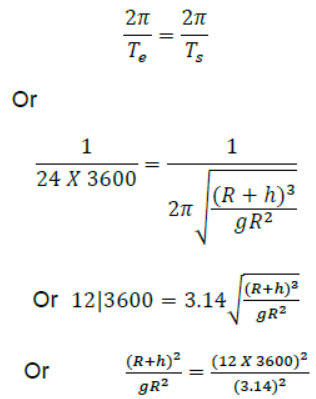
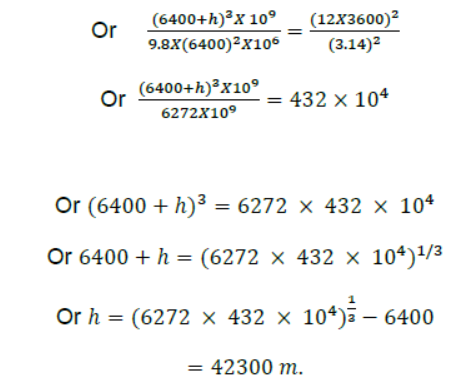
(b)Time taken from north pole to equator = (1/2) t

Question. Derive an expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the center.
Answer . A small section of rod is considered at ‘x’ distance mass of the element = (M/L).
dx = dm


Every object in the universe attracts every other object with a force which is called the force of gravitation.
Gravitation is one of the four classes of interactions found in nature.
These are
(i) the gravitational force
(ii) the electromagnetic force
(iii) the strong nuclear force (also called the hadronic force).
(iv) the weak nuclear forces.
Although, of negligible importance in the interactions of elementary particles, gravity is of primary importance in the interactions of objects. It is gravity that holds the universe together.
Newton’s Law of Gravitation
Gravitational force is a attractive force between two masses m1 and m2 separated by a distance r.
The gravitational force acting between two point objects is proportional to the product of their masses and inversely proportional to the square of the distance between them.

Gravitational force.
where G is universal gravitational constant.
The value of G is 6.67 X 10-11 Nm2 kg-2 and is same throughout the universe.
The value of G is independent of the nature and size of the bodies well as the nature of the
medium between them.
Dimensional formula of Gis [M-1L3T-2].
Important Points about Gravitation Force
(i) Gravitational force is a central as well as conservative force.
(ii) It is the weakest force in nature.
(iii) It is 1036 times smaller than electrostatic force and 10’l8times smaller than nuclear force.
(iv) The law of gravitational is applicable for all bodies, irrespective of their size, shape and position.
(v) Gravitational force acting between sun and planet provide it centripetal force for orbital motion.
(vi) Gravitational pull of the earth is called gravity.
(vii) Newton’s third law of motion holds good for the force of gravitation. It means the gravitation forces between two bodies are action-reaction pairs.
Following three points are important regarding the gravitational force
(i) Unlike the electrostatic force, it is independent of the medium between the particles.
(ii) It is conservative in nature.
(iii) It expresses the force between two point masses (of negligible volume). However, for external points of spherical bodies the whole mass can be assumed to be concentrated at its centre of mass.
Note Newton’s law of gravitation holde goods for object lying at uery large distances and also at very short distances. It fails when the distance between the objects is less than 10-9 m i.e., of the order of intermolecular distances.
Acceleration Due to Gravity
The uniform acceleration produced in a freely falling object due to the gravitational pull of the earth is known as acceleration due to gravity.
It is denoted by g and its unit is m/s2. It is a vector quantity and its direction is towards the centre of the earth.
The value of g is independent of the mass of the object which is falling freely under gravity.
The value of g changes slightly from place to place. The value of g is taken to be 9.8 m/s2 for all practical purposes.
The value of acceleration due to gravity on the moon is about. one sixth of that On the earth and on the sun is about 27 times of that on the earth.
Among the planets, the acceleration due to gravity is minimum on the mercury.
Relation between g and a is given by
g = Gm / R2
where M = mass of the earth = 6.0 * 1024 kg and R = radius of the earth = 6.38 * 106 m.
Acceleration due to gravity at a height h above the surface of the earth is given by
gh = Gm / (R+h)2 = g (1 – 2h / R)
Factors Affecting Acceleration Due to Gravity
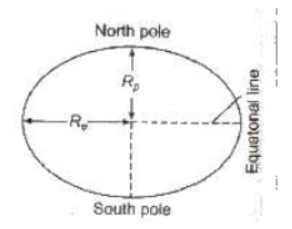
(i) Shape of Earth Acceleration due to gravity g &infi; 1 / R2 Earth is elliptical in shape. Its diameter at poles is approximately 42 km less than its diameter at equator.
Therefore, g is minimum at equator and maximum at poles.
(ii) Rotation of Earth about Its Own Axis If ω is the angular velocity of rotation of earth about its own axis, then acceleration due to gravity at a place having latitude λ is given by
g’ = g – Rω2 cos2 λ
At poles λ = 90° and g’ = g
Therefore, there is no effect of rotation of earth about its own axis at poles.
At equator λ = 0° and g’ = g – Rω2

The value of g is minimum at equator
If earth stapes its rotation about its own axis, then g will remain unchanged at poles but increases by Rω2at equator.
(iii) Effect of Altitude The value of g at height h from earth’s surface
g’ = g / (1 + h / R)2
Therefore g decreases with altitude.

(iv) Effect of Depth The value of gat depth h A from earth’s surface
g’ = g * (1 – h / R)
Therefore g decreases with depth from earth’s surface.
The value of g becomes zero at earth’s centre.

Gravitational Field
The space in the surrounding of any body in which its gravitational pull can be experienced by other bodies is called gravitational field.
Intensity of Gravitational Field
The gravitational force acting per unit mass at Earth any point in gravitational field is called intensity of gravitational field at that point.
It is denoted by Eg or I.
Eg or I = F / m

Intensity of gravitational field at a distance r from a body of mass M is given by
Eg or I = GM / r2
It is a vector quantity and its direction is towards the centre of gravity of the body.
Its S1 unit is N/m and its dimensional formula is [LT-2].
Gravitational mass Mg is defined by Newton’s law of gravitation.
Mg = Fg / g = W / g = Weight of body / Acceleration due to gravity
∴ (M1)g / (M2)g = Fg1g2 / Fg2g1
Gravitational Potential
Gravitational potential at any point in gravitational field is equal the work done per unit mass in bringing a very light body from infinity to that point.
It is denoted by Vg.
Gravitational potential, Vg = W / m = – GM / r
Its SI unit is J / kg and it is a scalar quantity. Its dimensional formula is [L3r-2].
Since work W is obtained, that is, it is negative, the gravitational potential is always negative.
Gravitational Potential Energy
Gravitational potential energy of any object at any point in gravitational field is equal to the
work done in bringing it from infinity to that point. It is denoted by U.
Gravitational potential energy U = – GMm / r
The negative sign shows that the gravitational potential energy decreases with increase in distance.
Gravitational potential energy at height h from surface of earth
Uh = – GMm / R + h = mgR / 1 + h/R

Satellite
A heavenly object which revolves around a planet is called a satellite. Natural satellites are those heavenly objects which are not man made and revolve around the earth. Artificial satellites are those neaven objects which are man made and launched for some purposes revolve around the earth.
Time period of satellite
T = 2π √r3 / GM
= 2π √(R + h)3 / g [ g = GM / R2
Near the earth surface, time period of the satellite
T = 2π √R3 / GM = √3π / Gp
T = 2π √R / g = 5.08 * 103 s = 84 min.
where p is the average density of earth.
Artificial satellites are of two types :
1. Geostationary or Parking Satellites
A satellite which appears to be at a fixed position at a definite height to an observer on earth is called geostationary or parking satellite.

Height from earth’s surface = 36000 km
Radius of orbit = 42400 km
Time period = 24 h
Orbital velocity = 3.1 km/s
Angular velocity = 2π / 24 = π / 12 rad / h
There satellites revolve around the earth in equatorial orbits.
The angular velocity of the satellite is same in magnitude and direction as that of angular
velocity of the earth about its own axis.
These satellites are used in communication purpose.
INSAT 2B and INSAT 2C are geostationary satellites of India.
2. Polar Satellites
These are those satellites which revolve in polar orbits around earth. A polar orbit is that orbit whose angle of inclination with equatorial plane of earth is 90°.

Height from earth’s surface = 880 km
Time period = 84 min
Orbital velocity = 8 km / s
Angular velocity = 2π / 84 = π / 42 rad / min.
There satellites revolve around the earth in polar orbits.
These satellites are used in forecasting weather, studying the upper region of the atmosphere, in
mapping, etc.
PSLV series satellites are polar satellites of India.
Orbital Velocity
Orbital velocity of a satellite is the minimum velocity required to the satellite into a given orbit
around earth.
Orbital velocity of a satellite is given by
vo = √GM / r = R √g / R + h
where, M = mass of the planet, R = radius of the planet and h = height of the satellite from
planet’s surface.
If satellite is revolving near the earth’s surface, then r = (R + h) =- R
Now orbital velocity, vo = √gR
= 7.92km / h
if v is the speed of a satellite in its orbit and vo is the required orbital velocity to move in the orbit, then
(i) If v < vo, then satellite will move on a parabolic path and satellite falls back to earth.
(ii) If V = vo then satellite revolves in circular path/orbit around earth.
(iii) If vo < V < ve then satellite shall revolve around earth in elliptical orbit.
Energy of a Satellite in Orbit
Total energy of a satellite
E = KE + PE
= GMm / 2r + (- GMm / r)
= – GMm / 2r
Binding Energy
The energy required to remove a satellite from its orbit around the earth (planet) to infinity is called binding energy of the satellite.
Binding energy of the satellite of mass m is given by
BE = + GMm / 2r
Escape Velocity
Escape velocity on earth is the minimum velocity with which a body has to be projected vertically upwards from the earth’s surface so that it just crosses the earth’s gravitational field
and never returns.
Escape velocity of any object
ve = √2GM / R
= √2gR = √8πp GR2 / 3
Escape velocity does not depend upon the mass or shape or size of the body as well as the
direction of projection of the body.
Escape velocity at earth is 11.2 km / s.
Some Important Escape Velocities
Heavenly body Escape velocity
Moon 2.3 km/s
Mercury 4.28 km/s
Earth 11.2 km/s
Jupiter 60 km/s
Sun 618 km/s
Neutron star 2 x 105 km/s
Relation between escape velocity and orbital velocity of the satellite
ve = √2 vo
If velocity of projection U is equal the escape velocity (v = ve), then the satellite will escape away following a parabolic path.
If velocity of projection u of satellite is greater than the escape velocity ( v > ve), then the satellite will escape away following a hyperbolic path.
Weightlessness
It is a situation in which the effective weight of the body becomes zero, Weightlessness is achieved
(i) during freely falling under gravity
(ii) inside a space craft or satellite
(iii) at the centre of the earth
(iv) when a body is lying in a freely falling lift.
Kepler’s Laws of Planetary Motion
(i) Law of orbit Every planet revolve around the sun in elliptical orbit and sun is at its one focus.

(ii) Law of area The radius vector drawn from the sun to a planet sweeps out equal areas in equal intervals of time, i.e., the areal velocity of the planet around the sun is constant.
Areal velocity of a planet
dA / dt = L / 2m = constant

where L = angular momentum and m = mass of the planet.
(iii) Law of period The square of the time period of revolution of planet around the sun is directly proportional to the cube semi-major axis of its elliptical orbit.
T2 &infi; a3 or (T1 / T2)2 = (a1 / a2)3
where, a = semi-major axis of the elliptical orbit.
Important Points
(i) A missile is launched with a velocity less than the escape velocity. The sum of its kinetic energy and potential energy is negative.
(ii) The orbital speed of jupiter is less than the orbital speed of earth.
(iii) A bomb explodes on the moon. You cannot hear the sound of the explosion on earth.
(iv) A bottle filled with water at 30°C and fitted with a cork is taken to the moon. If the cork is opened at the surface of the moon then water will boil.
(v) For a satellite orbiting near earth’s surface
(a) Orbital velocity = 8 km / s
(b) Time period = 84 min approximately
(c) Angular speed ω = 2π / 84 rad / min = 0.00125 rad / s
(vi) Inertial mass and gravitational mass
(a) Inertial mass = force / acceleration
(b) Gravitational mass = weight of body / acceleration due to gravity
(c) They are equal to each other in magnitude.
(d) Gravitational mass of a body is affected by the presence of other bodies near it. Inertial mass of a body remains unaffected by the presence of other bodies near it.

We hope the above Gravitation Class 11 Physics are useful for you. If you have any questions then post them in the comments section below. Our teachers will provide you an answer. Also refer to MCQ Questions for Class 11 Physics


