Please refer to Waves Class 11 Physics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Physics books for Class 11. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 11 Physics Waves Notes and Questions
Angular wave number: It is phase change per unit distance.
Relation between velocity, frequency and wavelength is given as :- V =uλ
Velocity of Transverse wave:-
(i)In solid molecules having modulus of rigidity ‘η ’ and density ‘ρ’ is
V = √n/p
(ii) In string for mass per unit length ’m’ and tension ‘T’ is √T/m
Velocity of longitudinal wave:-
(i) in solid V = √Y/ P , Y= young’s modulus
(ii) in liquid V = √K/ P , K= bulk modulus
(iii) in gases V= √K/P , K= bulk modulus
According to Newton’s formula: When sound travels in gas then changes take place in the medium are isothermal in nature. V = √P/P
According to Laplace: When sound travels in gas then changes take place in the medium are adiabatic in nature.
V = √PY/P ‘Where Y = Cp /Cv
Factors effecting velocity of sound :-
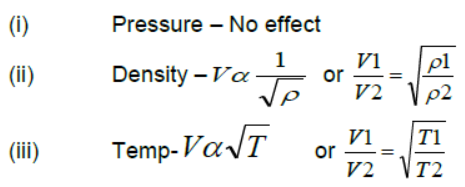
Effect of humidity :– sound travels faster in moist air
(iv) Effect of wind –velocity of sound increasing along the direction of wind.
Wave equation:– if wave is travelling along + x-axis
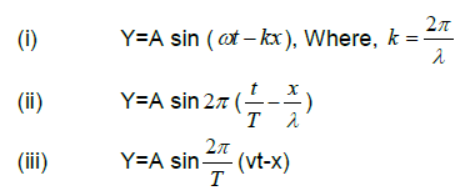
If wave is travelling along –ve x- axis
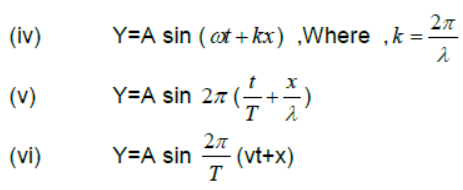
Phase and phase difference
Phase is the argument of the sine or cosine function representing the wave.
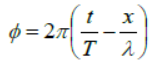
Relation between phase difference (ΔΦ) and time interval (Δt ) is ΔΦ = -2π/T Δt
Relation between phase difference ( Δp ) and path difference ( Δx ) is ΔΦ = -2π /λ Δx
Equation of stationary wave:-
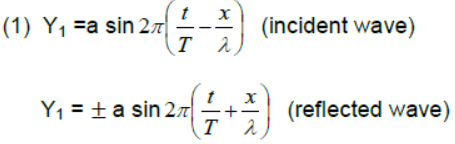
Stationary wave formed
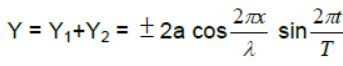
(2) For (+ve) sign antinodes are at x=
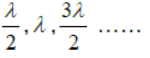
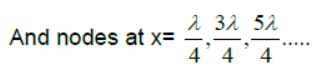
(3) For (-ve) sign antinodes are at x=
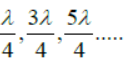
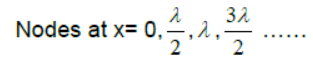
(4) Distance between two successive nodes or antinodes are λ/2 and that between nodes and nearest antinodes is λ/4
(5) Nodes-point of zero displacement-
Antinodes- point of maximum displacement
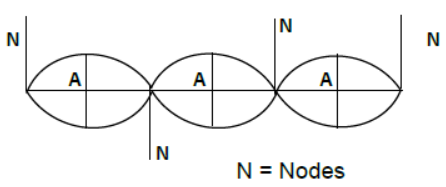
A = Antinodes
Mode of vibration of strings:-

ORGANPIPES
1. In an organ pipe closed at one end only odd harmonics are present

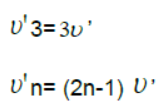
3. Resonance tube: If L1 and L2 are the first and second resonance length with a tuning fork of frequency ‘U ’then the speed of sound. v = 4ν(L1 + 0.3D ) Where ,D=internal diameter of resonance tube
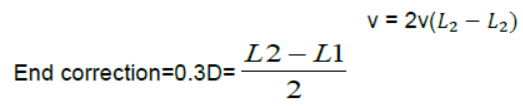
Beats formation
1. Beat frequency = No. of beats per second = Difference in frequency of two sources.
b = v1 – v2
2. v2 =v1 ± b
3. If the prong of tuning fork is filed, its frequency increases. If the prong of a tuning fork is loaded with a little way, its frequency decreases. These facts can be used to decide about + or – sign in the above equation.
Doppler effect in sound
1. If V, Vo, Vs, and Vm are the velocity of sound , observes, source and medium respectively, then the apparent frequency
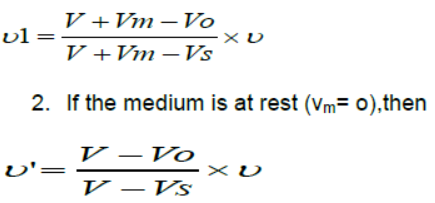
3. All the velocity are taken positive with source to observer (S→O) direction and negative in the opposite (S→O) direction
Question and Answer :
Question. A girl is swinging in the sitting position. How will the period of the swing change if she stands up? 4
Answer: The girl and the swing together constitute a pendulum of time period As the girl stands up her centre of gravity is raised. The distance between the point of suspension and the centre of gravity decreases i.e. length ‘l’ decreases .Hence the time period ‘T’ decreases.
Question. The maximum velocity of a particle, executing S.H.M with amplitude of 7mm is 4.4 m/s. What is the period of oscillation?
Answer:
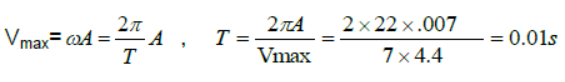
Question. Why the longitudinal wave are also called pressure waves?
Answer: Longitudinal wave travel in a medium as series of alternate compressions and rare fractions i.e. they travel as variations in pressure and hence are called pressure waves.
Question. How does the frequency of a tuning fork change, when the temperature is increased? 7
Answer: As the temperature is increased, the length of the prong of a tuning fork increased .This increased the wavelength of a stationary waves set up in the tuning fork. As frequency,
Question. An organ pipe emits a fundamental node of a frequency 128Hz. On blowing into it more strongly it produces the first overtone of the frequency 384Hz. What is the type of pipe –Closed or Open?
Answer: The organ pipe must be closed organ pipe, because the frequency the first overtone is three times the fundamental frequency.
Question. Which of the following relationships between the acceleration ‘a’ and the displacement ‘x’ of a particle involve simple harmonic motion?
(a) a=0.7x (b) a=-200x2 (c) a = -10x (d) a=100x3
Ans: – (c) reprent SHM.
Question. Can a motion be periodic and not oscillatory?
Answer: Yes, for example, uniform circular motion is periodic but not oscillatory.
Question. Can a motion be periodic and not simple harmonic? If your answer is yes, give an example and if not, explain why?
Answer: Yes, when a ball is doped from a height on a perfectly elastic surface ,the motion is oscillatory but not simple harmonic as restoring force F=mg=constant and not F∝ -x, which is an essential condition for S.H.M.
Question. All harmonic are overtones but all overtones are not harmonic. How?
Answer: The overtones with frequencies which are integral multiple of the fundamental frequency are called harmonics. Hence all harmonic are overtones. But overtones which are non-integrals multiples of the fundamental frequency are not harmonics.
Question. What is the factor on which pitch of a sound depends?
Answer: The pitch of a sound depends on its frequency.
Question. Does the function y = sin2ωt represent a periodic or a S.H.M? What is period of motion?
Answer: Displacement y = sin2ωt
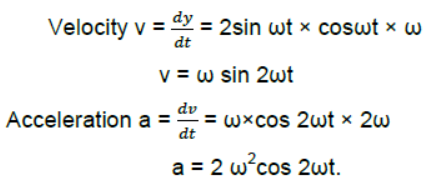
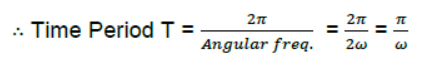
As the acceleration is not proportional to displacement y, the given function does not represent SHM. It represents a periodic motion of angular frequency 2ω.
Question. All trigonometric functions are periodic, but only sine or cosine functions are used to define SHM. Why?
Answer. All trigonometric functions are periodic. The sine and cosine functions can take value between -1 to +1 only. So they can be used to represent a bounded motion like SHM. But the functions such as tangent, cotangent, secant and cosecant can take value between 0 and ∞ (both negative and positive). So these functions cannot be used to represent bounded motion like SHM.
Question. A simple Harmonic Motion is represented by d2x/dt2 +αx = 0. What is its time period?
Answer:
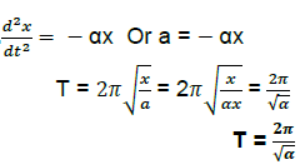
Question. The Length of a simple pendulum executing SHM is increased by 2.1%. What is the percentage increase in the time period of the pendulum of increased length?
Answer:
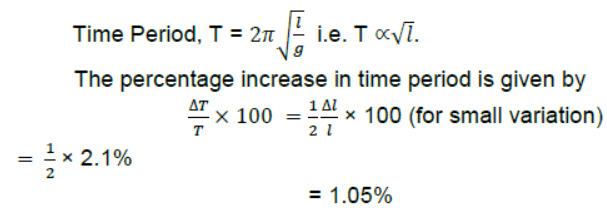
Question. A simple Harmonic motion has an amplitude A and time period T. What is the time taken to travel from x = A to x = A/2.
Answer: Displacement from mean position =
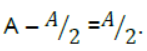
When the motion starts from the positive extreme position, y = A cosωt.
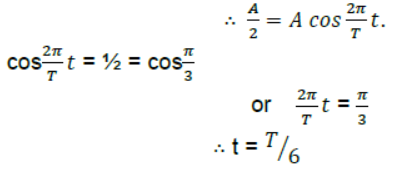
Question. At what points is the energy entirely kinetic and potential in S.H.M? What is the total distance travelled by a body executing S.H.M in a time equal to its time period, if its amplitude is A?
Answer: The energy is entirely kinetic at mean position i.e. at y=0. The energy is
entirely potential at extreme positions i.e.
y = ± A
Total distance travelled in time period T = 2A + 2A = 4A.
Question. A simple pendulum consisting of an inextensible length ‘l’ and mass ‘m’ is oscillating in a stationary lift. The lift then accelerates upwards with a constant acceleration of 4.5 m/s2. Write expression for the time period of simple pendulum in two cases. Does the time period increase, decrease or remain the same, when lift is accelerated upwards?
Answer: When the lift is stationary, T = 2π √1/g

Question. An open organ pipe produces a note of frequency 5/2 Hz at 150C, calculate the length of pipe. Velocity of sound at 00C is 335 m/s.
Answer: Velocity of sound at 150C
V=V0+0.61xt =335+0.61×15 =344.15 m/s. (Thermal coefficient
of velocity of sound wave is .61/0C)
Fundamental frequency of an organ pipe
Question. An incident wave is represented by Y(x, t)=20sin(2x-4t).Write the expression for reflected wave
(i) From a rigid boundary
(ii) From an open boundary.
Ans.(i) The wave reflected from a rigid boundary is
Y (x, t) = -20sin (2x+4t)
(i)The wave reflected from an open boundary is
Y (x, t) = 20sin (2x+4t)
Explain why
(i) in a sound wave a displacement node is a pressure antinode and vice- versa
(ii) The shape of pulse gets- distorted during propagation in a dispersive medium.
Answer: (i) At a displacement node the variations of pressure is maximum. Hence
displacement node is the a pressure antinode and vice-versa.
(ii)When a pulse passes through a dispersive medium the wavelength of wave changes.
So, the shape of pulse changes i.e. it gets distorted.
Question. Find the ratio of velocity of sound in hydrogen gas Ƴ 7 /5 to that in helium gas Ƴ 5 /3 at the same temperature. Given that molecular weight of hydrogen and helium are 2 and 4 respectively.
Answer:
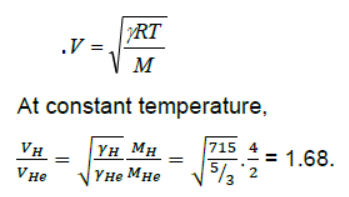
Question. The equation of a plane progressive wave is, y = 10sin2π(t – 0.005x) where y & x are in cm & t in second. Calculate the amplitude, frequency, wavelength & velocity of the wave.
Answer:
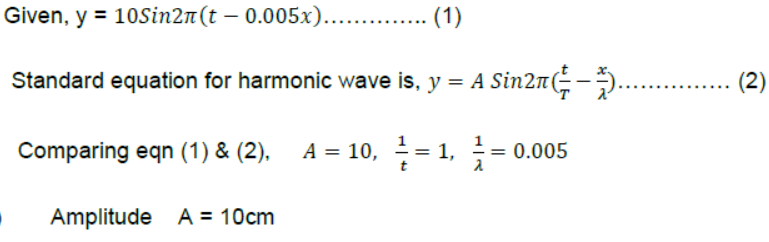
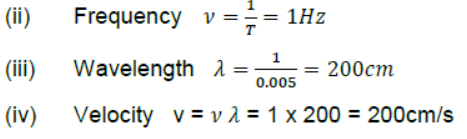
Question. Write displacement equation respecting the following condition obtained in SHM.
Amplitude = 0.01m
Frequency = 600Hz
Initial phase = π /6
Answer:
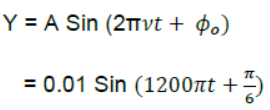
Question. The amplitude of oscillations of two similar pendulums similar in all respect are 2cm & 5cm respectively. Find the ratio of their energies of oscillations.
Answer:
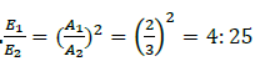
Question. What is the condition to be satisfied by a mathematical relation between time and displacement to describe a periodic motion?
Answer: A periodic motion repeats after a definite time interval T. So,
y(t) = y (t + T) = Y(t + 2T) etc.
Question. A spring of force constant 1200N/m is mounted horizontal table. A mass of 3Kg is attached to the free end of the spring, pulled sideways to a distance of 2.0cm and released.
(i) What is the frequency of oscillation of the mass?
(ii) What is the maximum acceleration of the mass?
(iii) What is the maximum speed of the mass?


Question. Write any three characteristics of stationary waves.
Answer: (i) in stationary waves, the disturbance does not advance forward. The conditions of crest and trough merely appear and disappear in fixed position to be followed by opposite condition after every half time period.
(ii) The distance between two successive nodes or antinodes is equal to half the wavelength.
(iii) The amplitude varies gradually from zero at the nodes to the maximum at the antinodes.
Question. Show that the speed of sound in air increased by .61m/s for every 10 C rise of temperature.
Answer:
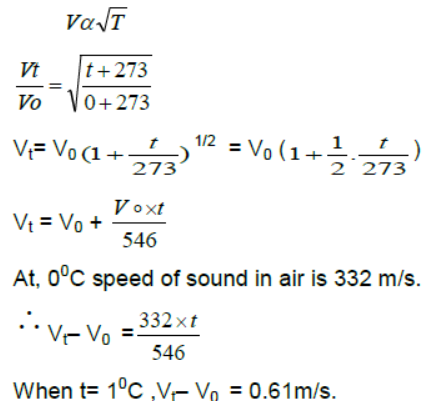
Question. Which of the following function of time represent, (a) simple harmonic (b) periodic but not SHM and (c) non periodic ?
Answer:

Question. (a) A light wave is reflected from a mirror. The incident & reflected wave superimpose to form stationary waves. But no nodes & antinodes are seen, why?
(b) A standing wave is represented by y=2ASinKxCoswt.If one of the component wave is y1 = Asin(ωt – kx) what is the equation of the second component wave?
Answer: (a) As is known, the distance between two successive nodes or two successive antinodes is λ/2 The wavelength of visible light is of the order of 10 -1m. As such as a
small distance cannot be detected by the eye or by a ordinary optical instrument.
Therefore, nodes and antinodes are not seen.
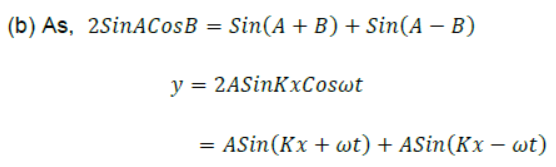
According to superposition principle,
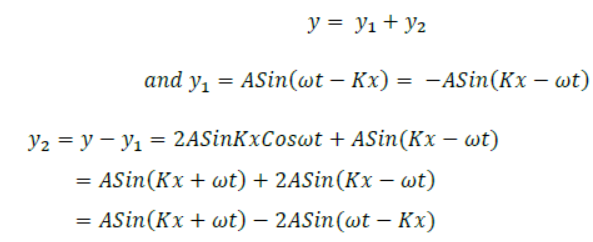
Question. Discuss Newton’s formula for velocity of sound in air. What correction was made to it by Laplace and why?
Answer: According to Newton the change in pressure & volume in air is an isothermal process. Therefore he calculated, v = √p/pon substituting the require value he found, the velocity of sound was not in close agreement with the observation value. Then Laplace pointed out the error in Newton’s formula. According to Laplace the change in pressure and volume is an adiabatic process. So he calculated the value of sound as, v = √yr/p on putting require value he found velocity of sound as 332m/s very closed to observed theory.
Question. A train stands at a platform blowing a whistle of frequency 400 Hz in still air.
(i) What is the frequency of the whistle heard by a man running
(a)Towards the engine 10 m/s.
(b) Away from the engine at 10 m/s?
(ii) What is the speed of sound in each case?
(iii) What is the wavelength of sound received by the running man in each case?
Take speed of sound in still air = 340 m/s.
Answer: (i) (a) When the man runs towards the engine


Question. Explain Doppler’s effect of sound. Derive an expression for the apparent frequency where the source and observer are moving in the same direction with velocity Vs and Vo respectively, with source following the observer.
Answer :
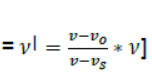
Question. For a travelling harmonic wave, y = 2cos(10t – 0.008x + 0.35) where x & y are in cm and t in second. What is the phase difference between oscillatory motions at two points separated by a distance of (i) 4cm (ii) 0.5m (iii) λ/2 (iv) 3λ /4 ?
Answer :
Question. (i) A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
(ii) A pipe 20 cm long is closed at one end. Which harmonic mode of the pipe is resonantly exited by a 430 Hz source? Will this same source be in resonance with the pipe if both ends are open? (Speed of sound = 340 m/s).
Answer : (i) For the fundamental mode

Hence source of frequency 430 Hz will not be in resonance with open organ pipe.
(a) Speed of longitudinal wave
Speed of longitudinal wave in a medium is given by
v = √E/p
where, E is the modulus of elasticity, p is the density of the medium.
Speed of longitudinal wave in a solid in the form of rod is given by
v = √Y/p
where, Y is the Young’s modulus of the solid,
p is the density of the solid.
Speed of longitudinal wave in fluid is given by
v = √B/p
where, B is the bulk modulus,
P is the density of the fluid.
(b) Newton’s formula
Newton assumed that propagation of sound wave in gas is an isothermal process. Therefore, according to Newton, speed of sound in gas is given by v = √P/p
where P is the pressure of the gas and p is the density of the gas.
According to the Newton’s formula, the speed of sound in air at S.T.P. is 280 m/s. But the experimental value of the speed of soundinairis 3 3 2 m s –1. Newton could not explain this large difference. Newton’s formula was corrected by Laplace.
(c) Laplace’s correction
Laplace assumed that propagation of sound wave in gas in an adiabatic process. Therefore, according to Laplace, speed of sound in a gas is given by
v = √YP/p
According to Laplace’s correction the speed of sound in air at S.T.P. is 331.3 m/s. This value agrees farily well with the experimental values of the velocity of sound in air at S.T.P.
WAVES TRAVELLING IN OPPOSITE DIRECTIONS
When two waves of same amplitude and frequency
travelling in opposite directions
y1 = A sin (kx – ωt)
y2 = A sin (kx + ωt)
interfere, then a standing wave is produced which is
given by,
y = y1 + y2
⇒ y = 2A sin kx cos ωt
Hence the particle at location x is oscillating in S.H.M. with angular frequency ω and amplitude 2A sin kx. As the amplitude depends on location (x), particles are oscillating with different amplitude.
Nodes : Amplitude = 0
2A sin kx = 0
x = 0, π/k, 2π/k…….
x = 0, λ/2, λ, 3λ/2, 2λ……..
Antinodes : Amplitude is maximum.
sin kx = ± 1
x = π/2k, 3π/2k
x = λ/4, 3λ/4, 5λ/4
Nodes are completely at rest. Antinodes are oscillating with maximum amplitude (2A). The points between a node and antinode have amplitude between 0 and 2 A. Separation between two consecutive (or antinodes) = λ/2.
Separation between a node and the next antinode=λ/4.
Nodes and antinodes are alternately placed.
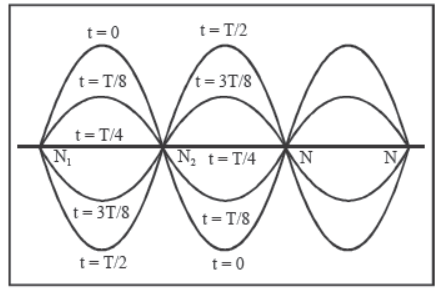
It is clear from the figure that since nodes are, at rest they don’t transfer energy. In a stationary wave, energy is not transferred from one point to the other.
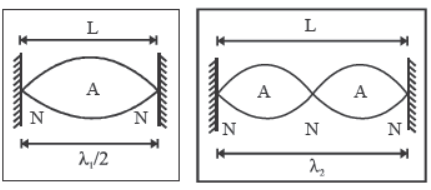
Vibrations in a stretched string
1. Fixed at both ends.
Transverse standing waves with nodes at both ends of the string are formed.
So, length of string, l = nλ/2 if there are (n + 1) nodes and n antinodes.
Frequency of oscillations is
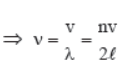
Fundamental frequency (x = 1)
0v = V 2L
It is also called first harmonic.
Second harmonic or first overtone
It is also called first harmonic.
Second harmonic or first overtone
0v = 2V 2L
The nth multiple of fundamental frequency is known as nth harmonic or (n – 1)th overtone.
2. Fixed at one end
Transverse standing waves with node at fixed end and antinode at open end are formed.
So, length of string l = (2n – 1) λ/4 if there are n nodes and n antinodes.
Frequency of oscillations
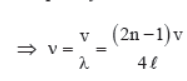
Fundamental frequency, (n = 1)
v 0 = V/4L
It is also called first harmonic.
First overtone or third harmonic.
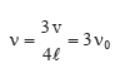
Only odd harmonics are possible in this case.
Vibrations in an organ pipe
1. Open Organ pipe (both ends open)
The open ends of the tube becomes antinodes because the particles at the open end can oscillate freely.
If there are (n + 1) antinodes in all,
length of tube, l = nλ/2
So, Frequency of oscillations is v = nv/2l
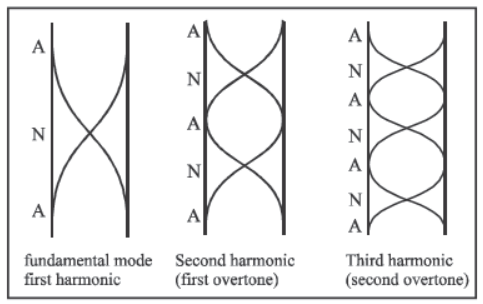
2. Closed organ pipe (One end closed)
The open end becomes antinode and closed end become a node.
If there are n nodes and n antinodes,
L = (2n – 1) λ/4
So frequency of oscillations is
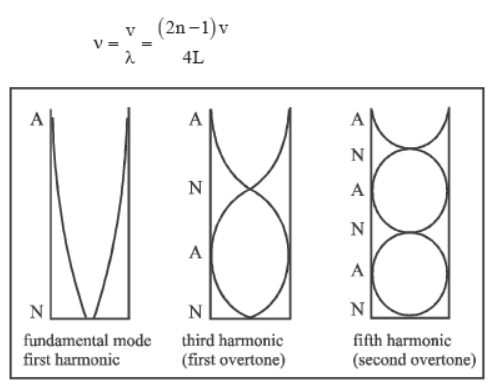
There are only odd harmonics in a tube closed at one end.
Waves having different frequencies
Beats are formed by the superposition of two waves of slightly different frequencies moving in the same direction. The resultant effect heard in this case at any fixed position will consist of alternate loud and weak sounds.

amplitude is 2A cos π (v1– v2) t.
As the amplitude term contains t, the amplitude varies
periodically with time.
For Loud Sounds : Net amplitude = ± 2A
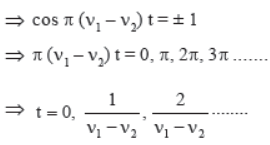
Hence the interval between two loud sounds is given as :
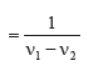
⇒ the number of loud sounds per second = v1 – v2
⇒ beat per second = v1 – v2
Note that v1 – v2 must be small (0 – 16 Hz) so that sound variations can be distinguished.
DOPPLER EFFECT
According to Doppler’s effect, whenever there is a relative motion between a source of sound and listener, the apparent frequency of sound heard by the listener is different from the actual frequency of sound emitted by the source.
Apparent frequency,
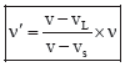
Sing Convention. All velocities along the direction S to L are taken as positve and all velocities along the direction L to S are taken as negative.
When the motion is along some other direction the component of velocity of source and listener along the line joining the source and listener is considered.
Special Cases :
(a) If the source is moving towards the listener but the listener is at rest, then vs is positive and vL = 0 (figure a). Therefore,
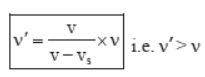
(b) If the source is moving away from the listener, but the listener is at rest, then vs is negative and vL = 0 (figure b). Therefore,
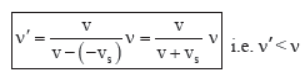
(c) If the source is at rest and listener is moving away from the source, the vs = 0 and vL is positive (figure c). Therefore,
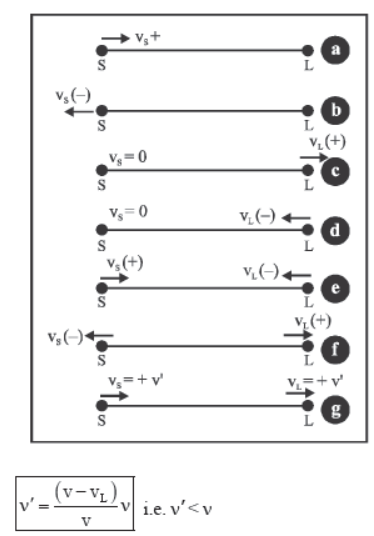
(d) If the source is at rest and listener is moving towards the source, then vs = 0 and vL is negative (figure d). Therefore,
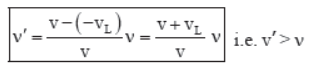
(e) If the source and listener are approaching each other, then vs is positive and vL is negative (figure e). Therefore,
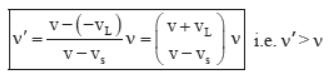
(f) If the source and listener are moving away from each other, then vs is negative and vL is positive, (figure f). Therefore,
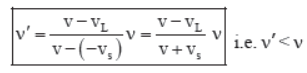
(g) If the source and listener are both in motion in the same direction and with same velocity, then vs = vL = v’ (say) (figure g). Therefore,
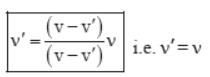
It means, there is no change in the frequency of sound heard by the listerner.
Ap par ent wavelength heard b y the o b ser ver is
CHARACTERISTICS OF SOUND
Loudness of sound is also called level of intensity of sound.
In decibel the loudness of a sound of intensity I is
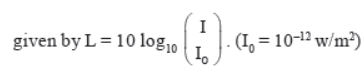
Pitch : It is pitch depends on frequency, higher the frequency higher will be the pitch and shriller will be the sound.

We hope the above Waves Class 11 Physics are useful for you. If you have any questions then post them in the comments section below. Our teachers will provide you an answer. Also refer to MCQ Questions for Class 11 Physics


