Check the below NCERT MCQ Class 12 Mathematics Chapter 11 Three Dimensional Geometry with Answers available with PDF free download. MCQ Questions for Class 12 Mathematics with Answers were prepared based on the latest syllabus and examination pattern issued by CBSE, NCERT and KVS. Our teachers have provided below Three Dimensional Geometry Mathematics Class 12 Mathematics MCQs Questions with answers which will help students to revise and get more marks in exams
Three Dimensional Geometry Class 12 Mathematics MCQ Questions with Answers
Refer below for MCQ Class 12 Mathematics Chapter 11 Three Dimensional Geometry with solutions. Solve questions and compare with the answers provided below
Question. The three planes x + y = 0, y + z = 0 and x + z = 0
(a) meet in a unique point
(b) meet in a line
(c) meet taken two at a time in parallel lines
(d) None of these
Answer
A
Question. The points (2, 3, 4), (−1, −2, 1) and (5, 8, 7) are
(a) formed an isosceles triangle
(b) formed an equilateral triangle
(c) collinear
(d) None of the above
Answer
C
Question. The direction cosines of the side AB of the ∆ ABC whose vertices are A( 3,5,-4), B (-1,1,2) ) and C (-5,-5,-2) are///3
(a) − 4/√17,-4/√17,6/√17
(b) −/√17,-2/√17,3/√17
(c) − 2/√17,2/√17,-3/√17
(d) None of these
Answer
B
Question. If a line makes angles 90°, 35°, 45° and with the positive x,y and z-axes respectively, then its direction cosines are
(a) 0-1/√2 and 1/2√
(b) 0,1/2 and -1/2
(c) 0,-1/2 and 1/√2
(d) 1,-1/2 and 1/√2
Answer
A
Question. If a line makes an angle of π/4 with each of y and z axes, then the angle which it makes with x-axis is
(a) π/2
(b) π/3
(c) π/4
(d) π/6
Answer
A
Question. The points P(4, 5, 10), Q(2, 3, 4) and R(1, 2, 1) − are three vertices of a parallelogram PQRS. The coordinates of S are
(a) (3, 4, 5)
(b) (4, 6, 5)
(c) (1, 1, 5)
(d) (1, 3, 5)
Answer
A
Question. If a line makes angles α β γ , and with the positive directions of the coordinate axes, then the value of sin2α+sin2 β+ sin2 y is
(a) 0
(b) 1
(c) 2
(d) −1
Answer
C
Question. A line makes angles α, β, γ and δ with the four diagonals of a cube, then cos2α + cos2 β+ cos2 y + cos2δ is equal to
(a) 1
(b) 4/3
(c) 3/4
(d) 4/5
Answer
B
Question. A line passes through the points ( 6, 7,-1) and (2,-3,1)) The direction cosines of the line so directed that the angle made by it with the positive direction of x-axis is acute, is
(a) 2/3,-2/3,-1/3
(b) −2/3,2/3.1/3
(c) 2/3,-2/3,1/3
(d) 2/3,2/3,1/3
Answer
A
Question. If the projection of a line segment on x,y and z-axes are 3,1 and √15 respectively then length of line segment is
(a) 5
(b) 4+ √15
(c) 5 +√2
(d) 6
Answer
A
Question. If a line makes angles α, β γ and with the axes, then cos2α+ cos2β+ cos2y is equal to
(a) −2
(b) −1
(c) 1
(d) 2
Answer
B
Question. O is the origin. OP makes an angle of 45° and 60° with the positive direction of x and y-axes respectively. OP = 12 units. Then, the coordinates of P are
(a) (6, 6, 6)
(b) (6, 6, −6)
(c) (6 √2, 6, ± 6)
(d) (6, ± 6, 6)
Answer
C
Question. If a line lies in the octant OXYZ and it makes equal angles with the axes, then
(a) l=m=n=1/√3
(b) l =m= n = ± 1/√3
(c) l =m=n=-1/√3
(d) l =m= n =± 1/√2
Answer
A
Question. If (1/2,1/3,n) are the direction cosines of a line, then the value of n is
(a) √23/6
(b) 23/6
(c) 2/3
(d) 3/2
Answer
A
Question. A line makes acute angles of α, β and γ with the coordinate axes such that cos α cos β = cos β=cos y=2/9 and cos y cos α =4/9, then cos α+ cos β+cos y is equal to
(a) 25/9
(b) 5/9
(c) 5/3
(d) 2/3
Answer
C
Question. Lines OA and OB are drawn from O with direction cosines proportional to (1,2, -1) and ( , ,3,-2,3), respectively. The direction ratios of the normal to the pane AOB are
(a) (4, 3, 2)
(b) (4,-3,-2)
(c) (-4,3,-2)
(d) (4,3,-2)
Answer
D
Question. If O is the origin and OP = 3 with direction ratios – 1, 2, – 2, then coordinates of P are
(a) (1, 2, 2)
(b) (– 1, 2, – 2)
(c) (– 3, 6, – 9)
(d) (-1/3, 2/3, 2/3)
Answer
B
Question. The direction cosines l m, and n of two lines are connected by the relations l+ m+ n = 0, lm = 0, then the angles between them is
(a) π /3
(b) π /4
(c) π /2
(d) 0
Answer
A
Question. The points (5,2,4), (6,-1,2) ) and ( 8,-7,k) are collinear, if k is equal to
(a) − 2
(b) 2
(c) 3
(d) − 1
Answer
A
Question. The vector equation of a plane which is at a distance of 7 units from the origin and normal to the vector
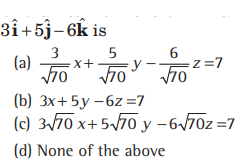
Answer
A
Question. The angle θ between two planes A1x + B1y + C1z + D1 =0 and A2x + B2y + C2z + D2 =0 is given by cos θ equal to
(a) A1A2 + B1B2 + C1C2
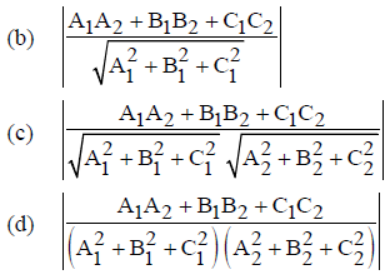
Answer
C
Question. The distance of a point (2, 5, –3) from the plane r . (6î – 3ĵ + 2k̂) = 4 is
(a) 13
(b) 13/7
(c) 13/5
(d) 37/7
Answer
B
Question. What is the condition for the plane ax + by + cz + d = 0 to be perpendicular to xy-plane ?
(a) a = 0
(b) b = 0
(c) c = 0
(d) a + b +c = 0
Answer
C
Question. The equation of the plane passing through three noncollinear points with position vectors a̅, b̅, c̅ is

Answer
B
Question. The shortest distance between the Z-axis and the line x + y + 2z – 3 = 0, 2x + 3y + 4z – 4 = 0 is
(a) 2
(b) 1/2
(c) 0
(d) 1
Answer
A
Question. Consider the following statements:
I. Equations ax + by + cz + d = 0, a’x + b’y + c’z + d’ = 0 represent a straight line.
II. Equation of the form x-α/l = y-β/m = z-γ/n represent a straight line passing through the point (α , β , γ)
and having direction ratio proportional to l, m, n.
Which of the statements given above is/are correct ?
(a) Only I
(b) Only II
(c) Both I and II
(d) Neither I nor II
Answer
C
Question. The line x-1/1 = y-2/-2 = z-1/3 and the plane x + 2y + z = 6 meet at
(a) no point.
(b) only one point.
(c) infinitely many points.
(d) none of these.
Answer
C
Question.
| Column-I (Planes) | Column-II (Their equations) |
| A. The plane which cut equal intercepts of unit length on the axes | by + cz + d = 0 |
| B. The plane through (2, 3, 4) and parallel to the plane x + 2y + 4z = 5. | x + y + z = 1 |
| C. The plane parallel to X-axis | x + 2y + 4z = 24 |
Codes
A B C
(a) 1 2 3
(b) 3 1 2
(c) 2 3 1
(d) 2 1 3
Answer
C
Question. Distance between the parallel planes 2x – y + 3z + 4 = 0 and 6x – 3y + 9z – 3 = 0 is:
(a) 5/√3
(b) 4/√6
(c) 5/√14
(d) 3/2√3
Answer
C
Question. Consider the following statements
Statement I: The angle between two planes x + 2y + 2z = 3 and –5 x + 3y + 4z = 9 is cos-1(19√2/30) .
Statement II: The angle between the line x-1/2 = y-2/1 = z+3/-2 and the plane x + y + 4 = 0 is 45°.
Choose the correct option.
(a) Statement I is true
(b) Statement II is true
(c) Both statements are true
(d) Both statements are false
Answer
B
Question. The lines x = ay + b, z = cy +d and x = a’y + b’, z = c’y +d’ are perpendicular if
(a) aa’ +bb’ + cc’ + 1 = 0
(b) aa’+bb’+1 = 0
(c) bb’+cc’+1 = 0
(d) aa’ + cc” +1 = 0
Answer
D
Question. Consider the following statements
Statement I : The angle between two planes is twice the angle between their normals.
Statement II : If θ is the angle between two planes, then 180 – θ is also the angle between same planes.
Choose the correct option.
(a) Statement I is true
(b) Statement II is true
(c) Both statements are true
(d) Both statements are false
Answer
B
Question. The vector equation of the symmetrical form of equation of straight line x-5/3 = y+4/7 = z-6/2 is

Answer
D
Question. The d.r. of normal to the plane through (1, 0, 0), (0, 1, 0) which makes an angle π/4 with plane x + y = 3 are
(a) 1, √2 ,1
(b) 1, 1, √2
(c) 1, 1, 2
(d) 2 , 1, 1
Answer
B
Question. Which of the following is/are true?
I. The vector equation of the line passing through the point (1, 2, –4) and perpendicular to the two lines x-8/3 = y+19/-16 = z-10/7 and x-15/3 = y-29/8 = z-5/-5 is r = (î + 2ĵ – 4kˆ ) + λ (2î + 3ĵ + 6kˆ )
II. If a plane has intercepts a, b, c and is at a distance of p units from the origin, then p2 = a2 + b2 + c2.
(a) Only I is true
(b) Only II are true
(c) Both I and III are true
(d) Neither I nor II is true
Answer
A
Question. If r = a1 + λb1 and r = a2 + μb2 are the equations of two lines, then cos θ =

Answer
B
Question.

Codes
A B C
(a) 1 3 2
(b) 2 3 1
(c) 3 1 2
(d) 2 1 3
Answer
C
Question. The distance of the point (–5, –5, –10) from the point of intersection of the line r . = 2î – ĵ + 2k̂ + λ (3î + 4ĵ+ 2k̂ )and the plane r· (î – ĵ + k̂)= 5 is
(a) 13
(b) 12
(c) 4 √15
(d) 10 √2
Answer
A
Question. Let L be the line of intersection of the planes 2x + 3y + z = 1 and x + 3y + 2z = 2. If L makes an angle α with the positive x-axis, then cos α equals
(a) 1
(b) 1/√2
(c) 1/√3
(d) 1/2
Answer
C
Question. The vector equation of the plane which is at a distance of 6/√29 from the origin and its normal vector from the origin is 2î – 3ĵ + k̂, is

(c) Both (a) and (b)
(d) None of the above
Answer
B
Question. The coordinates of the point where the line through the points A (3, 4, 1) and B (5, 1, 6) crosses the XY – plane are
(a) (13/5 , 23/5 , 0)
(b) (-13/5 , 23/5 , 0)
(c) (13/5 , -23/5 , 0)
(d) (-13/5 , -23/5 , 0)
Answer
A
Question. If a line makes an angle of π / 4 with the positive directions of each of x- axis and y- axis, then the angle that the line makes with the positive direction of the z-axis is
(a) π /4
(b) π /2
(c) π /6
(d) π /3
Answer
B
Question. The shortest distance between the lines x = y + 2 = 6z – 6 and x + 1 = 2y = – 12z is
(a) 1/2
(b) 2
(c) 1
(d) 3/2
Answer
B
Question. A plane meets the coordinate axes in points A, B, C and the centroid of the triangle ABC is (α, β, ϒ) . The equation of the plane is
(a) x/α + y/β + z/ϒ = 3
(b) αx +βy + ϒz = 3αβϒ
(c) x/α + y/β + z/ϒ =1/2
(d) None of these
Answer
A
Question. The locus of a point, such that the sum of the squares of its distances from the planes x + y + z = 0, x – z =0 and x – 2y + z = 0 is 9, is
(a) x2 + y2 + z2 = 3
(b) x2 + y2 + z2 = 6
(c) x2 + y2 + z2 = 9
(d) x2 + y2 + z2 =12
Answer
C
Question. If the angle θ between the line x+1/1 = y-1/2 = z-2/2 and sin θ = 1/3 then the value of λ is
(a) 5/3
(b) -3/5
(c) 3/4
(d) -4/3
Answer
A
Question. The lines whose vector equations are

are perpendicular for all values of λ and μ if p =
(a) 1
(b) –1
(c) – 6
(d) 6
Answer
D
Question. The sine of the angle between the straight line x-2/3 = y-3/4 = z-4/5 and the plane 2x – 2y + z = 5 is
(a) 10/6√5
(b) 4/5√2
(c) 2/√3/5
(d) √2/10
Answer
D
Question. The equation of two lines through the origin, which intersect the line x-3/2 = y-3/1 = z/1 at angles of π/3 each, are
(a) x/1 = y/2 = z/1 ; x/1 = y/1 = z/2
(b) x/1 = y/2 = z/-1 ; x/1 = y/1 = z/-2
(c) x/1 = y/2 = z/-1 ; x/1 = y/-1 = z/-2
(d) None of the above
Answer
B
Question. What is the length of the projection of 3î + 4ĵ+5kˆ on the xy-plane ?
(a) 3
(b) 5
(c) 7
(d) 9
Answer
B
Question. What is the angle between the line 6x = 4y = 3z and the plane 3x + 2y – 3z = 4 ?
(a) 0
(b) π/6
(c) π/3
(d) π/2
Answer
A
Question. A rectangular parallelopiped is formed by drawing planes through the points (–1, 2, 5) and (1, –1, –1) and parallel to the coordinate planes. The length of the diagonal of the parallelopiped is
(a) 2
(b) 3
(c) 6
(d) 7
Answer
D
Question. The distance between the lines given by

(a) √59/14
(b) √59/7
(c) √118/7
(d) √59/7
Answer
B
Question. If O be the origin and the coordinates of P be (1, 2, –3), then the equation of the plane passing through P and perpendicular to OP is
(a) x + 2y + 3z = –5
(b) x + 2y + 3z = – 14
(c) x + 2y – 3z =14
(d) x + 2y – 3z =5
Answer
C
Question. Four points (0, –1, –1) (–4, 4, 4) (4, 5, 1) and (3, 9, 4) are coplanar. Find the equation of the plane containing them.
(a) 5x + 7y + 11z – 4 = 0
(b) 5x – 7y + 11z + 4 = 0
(c) 5x – 7y –11z – 4 = 0
(d) 5x + 7y – 11z + 4 = 0
Answer
B
Question. The points A(1, 2, 3), B (–1, –2, –3) and C(2, 3, 2) are three vertices of a parallelogram ABCD. The equation of CD is
(a) x/1 = y/2 = z/2
(b) x+2/1 = y+3/2 = z-2/2
(c) x/2 = y/3 = z/2
(d) x-2/1 = y-3/2 = z-2/2
Answer
D
Question. A variable plane remains at constant distance p from the origin.If it meets coordinate axes at points A, B, C then the locus of the centroid of ΔABC is
(a) x-2 + y-2 + z-2 = 9p-2
(b) x-3 + y-3 + z-3 =9p-3
(c) x2 + y2 + z2 = 9p2
(d) x3 + y3 + z3 = 9p3
Answer
A
Question. Two lines r̅ = a̅1 + λb̅1 and r̅ = a̅2 + μb̅2 are said to be coplanar, if
(a) (a2 – a1) . (b1 × b2) = 0

where (x1, y1, z1) are the coordinates of a point on any of the line and a1, b1, c1 and a2, b2, c2 are the direction ratio of b1 and b2
(c) Both (a) and (b)
(d) None of the above
Answer
A
Question. The lines in a space which are neither intersecting nor parallel, are called
(a) concurrent lines
(b) intersecting lines
(c) skew lines
(d) parallel lines
Answer
C