Please refer to Surface Area And Volume Class 10 Mathematics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Mathematics books for Class 10. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 10 Mathematics Surface Area And Volume Notes and Questions
Please refer to Surface Area and Volume Class 10 Mathematics notes and questions with solutions below. These revision notes and important examination questions have been prepared based on the latest Mathematics books for Class 10. You can go through the questions and solutions below which will help you to get better marks in your examinations.
Class 10 Mathematics Surface Area and Volume Notes and Questions
Surface Areas and Volumes
Curved Surface Area Of Combination Of Solids
We know how to find the curved surface areas of three-dimensional figures such as cone, cylinder, sphere, etc. Now, we will learn to find out the curved surface area of a combination of solids.
Let us consider the following figure.
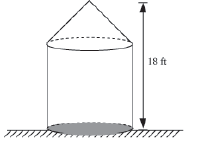
The given figure shows a temple. In this figure, the base of the temple is a right circular cylinder and the top is a right circular cone. The height of the conical part is half the height of the cylindrical part and the radius of the base of the temple is 2 ft more than the height of the conical part. The temple has to be plastered from outside at the rate of Rs 5 per square foot.
Can we find the approximate cost of plastering the temple from outside?
In order to find the cost, we have to find the curved surface area of the temple. By adding the curved surface areas of cone and cylinder, we can obtain the curved surface area of the temple.
First of all, let us review the formulae to find the curved surface areas of different solids.The formulae for different solids are given in the following table.

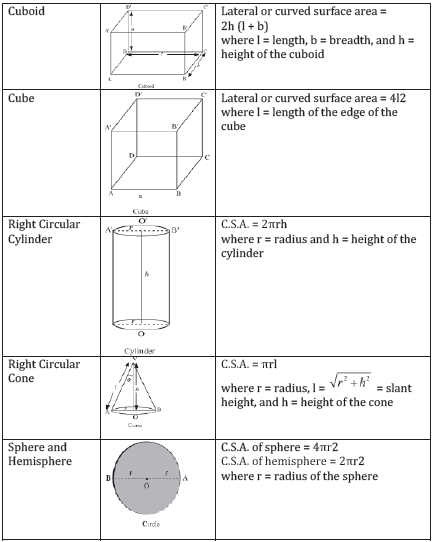
In this way, we can find the curved surface area of a combination of solids. Now, let us solve some more examples to understand the concept better.
Example 1: A toy is in the form of a hemisphere mounted by a cone. The diameter of the hemisphere is 21 cm and height of the whole toy is 24.5 cm. If the surface of the toy is painted at the rate of Rs 1 per 5 cm2, then find the cost required to paint the entire toy.
Solution:
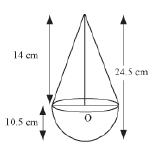
It is given that the diameter of the hemisphere is 21 cm.
∴ Radius of the hemisphere, r = 10.5 cm
Radius of the base of the cone, r = 10.5 cm
From the figure, height of cone, h = 24.5 − 10.5 = 14 cm
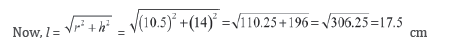
∴ Surface area of the toy = C.S.A. of hemisphere + C.S.A. of cone
= 2πr2 + πrl
= πr (2r + l)
= 22/7×10.5×(2×10.5+17.5)
= 22 × 1.5 × 38.5
= 1270.5 cm2
∴ Cost required for painting = 1270.5 × 1/5 = Rs 254 approximately
Example 2: The given figure shows a post office box. It was painted with red colour and it is observed that the ratio between the cost of painting the hemispherical part and the cylindrical part is 2:7. What is the ratio between the height of the box and the radius of the hemispherical part?

Solution:
As the box is painted with a constant cost, irrespective of the hemispherical part and the cylindrical part, we obtain

Thus, the ratio between the height of the box and the radius of the hemispherical part is 9:2.
Example 3: A tent is in the shape of a cylinder surmounted by a conical top. If the ratio of the height of the cylinder, the radius of cylinder, and the height of the cone is 8:4:3 and the cost of canvas required for making the tent is Rs 10560 at the rate of Rs 10 per m2, then find the height of the tent.
Solution:
Let us consider, height of cylinder = h’, radius of cylinder = r, and height of cone = h
Let h’ = 8x, r = 4x, and h = 3x
Amount of canvas = 10560/10 =1056 m2
However, amount of canvas = C.S.A. of cylinder + C.S.A. of cone
1056 = 2πrh’ + πrl
1056 = πr (2h’ + l)
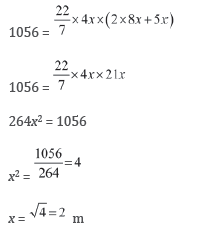
Height of tent = height of cylindrical part + height of conical part
= 8x + 3x
= 11x
= 11× 2
= 22
Thus, the height of the tent is 22 m.
Board question(s) related to this lesson:
Total Surface Areas Of Combination Of Solids
Total surface area of any solid is the sum of its curved surface area and bases. In many situations, we are required to find the total surface area of a combination of solids. Let us
consider such a situation.
The largest possible hemisphere is taken out from a cube of side 10 cm. Can we find out the total surface area of the remaining solid?
To find it, consider the following figure.
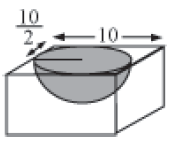
From the cube, the largest hemisphere is taken out.
That means, diameter of hemisphere = edge of the cube = 10 cm
∴ Radius of the hemisphere = 10/2= 5cm
Total Surface area of the remaining solid = T.S.A. of cube without the circular base + C.S.A. of hemisphere
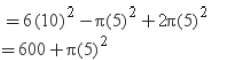
= 678.5 cm2
Thus, the required area is 678.5 cm2.
Let us solve some more examples to understand the concept better.
Example 1: From a cylinder of radius 7 m and height 24 m, a cone of same radius and same height is taken out. Find the surface area of the remaining part. If the inner portion of this remaining part is painted in pink colour at the rate of Rs 23 per 5 m2 and the exterior portion is painted in green colour at the rate of Rs 40 per 11 m2, then find the total cost required to paint such a solid.
Solution:
It is given that the radius and height of the cylinder and cone are the same.
Let radius r = 7 m and height h = 24 m
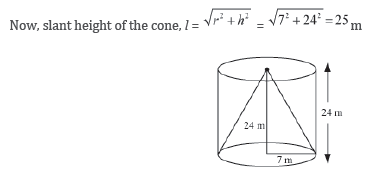
After taking out the cone from the cylinder,
T.S.A. of remaining outer part = C.S.A. of cylinder + Area of Circle
= 2πrh + πr2
= πr (2h + r)
= 22/7×7(2×24+7)
= 22 × 55
= 1210 m2
T.S.A. of remaining inner part = C.S.A. of cone
= πrl
= 22/7×7×25
= 550 m2
Cost of painting the exterior part = 1210 × 40/11= Rs 4400
Cost of painting the interior part = 550 × 23/5=Rs 2530
∴ Cost of painting the remaining solid = 4400 + 2530 = Rs 6930
Thus, the required cost is Rs 6930.
Example 2: A right triangle, whose perpendicular sides are 30 cm and 40 cm, is made to revolve about its hypotenuse. Find the surface area of the double cone so
obtained.
Solution:
Let ABD be the right-angled triangle such that AB = 30 cm and AD = 40 cm
Using Pythagoras theorem, we obtain
BD2 = AB2 + AD2
BD2 = 302+402+=900+1600=2500
BD = √2500=50cm
Let OB = x and OA = y
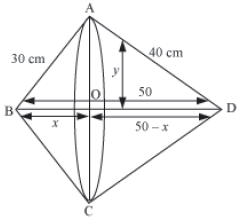
Applying Pythagoras theorem in ΔAOB, we obtain
OA2 + OB2 = AB2
x2 + y2 = 302
y2 = 900 − x2 … (1)
Applying Pythagoras theorem in ΔAOD, we obtain
OA2 + OD2 = AD2
y2 + (50 − x) 2 = 402
900 − x2 + 2500 + x2 − 100x = 1600 {From equation (1), we have y2 = 900 − x2}
100x = 1800
x = 18
On putting this value in equation (1), we obtain
y2 = 900 − x2 = 900 − 182 = 900 − 324 = 576
y =√576 =24 cm
Here, y is the radius of both the cones.
Now, surface area of the solid = C.S.A. of cone ABC + C.S.A. of cone ADC
= π × 24 × 30 + π × 24 × 40
= 1680 π
= 1680 × 22/7
= 5280 cm2
Thus, the surface area of the double cone so obtained is 5280 cm2.
Example 3: The inner and outer radii of a cylindrical iron container are 10 cm and 11 cm respectively. The thickness of the base is 1.5 cm and the total height of the container is 21.5 cm. Find the cost, if the container has to be thoroughly electroplated with silver metal at the rate of 70 paise per cm2.
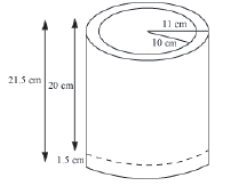
Solution:
To find out the cost, we have to find out the T.S.A. of the container.
Height of the base, h = 1.5 cm
∴Height of the hollow cylinder, H = 21.5 − 1.5 = 20 cm
External radius, R = 11 cm and internal radius, r = 10 cm
T.S.A. of the container = Outer C.S.A. of hollow cylinder + Inner C.S.A. of hollow cylinder +
Area of the ring + C.S.A. of solid cylinder + Area of inner base + Area of outer base
= 2π RH + 2πrH + π (R2 − r2) + 2πRh + πr2 + πR2
= 2π (R + r) H + π (R2 − r2) + π (2Rh + r2 + R2)
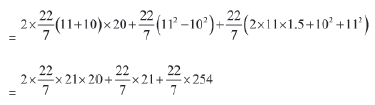
= 2640 + 66 + 5588/7
= 24530/7 cm2
∴ Cost of electroplating = 24530/7 × 70 = 245300 paise = Rs 2453
Thus, the required cost is Rs 2453.
Volume Of Combination Of Solids
We come across many figures in our daily life that are made up of two or more solid figures.
Let us consider such an example.
A company produces metallic solid toys that are in the shape of a cylinder with one hemisphere and one cone stuck to their opposite ends. The length of the entire toy is 30 cm; the diameter of the cylinder is 14 cm, while the height of the cone is 10 cm.
Can we find out how much metal should the company order to make 200 toys of this type?
In this way, we can find the volume of any solid figure which is formed by combining two or more basic solids. Let us now look at some more examples.
Example 1: A largest cone is to be taken out from a cube of edge 15 cm. Find the volume of the remaining portion. (Use π = 3.14)
Solution:
The figure can be drawn as follows:
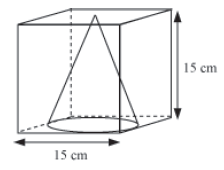
It is given that length of the cube, l = 15 cm
The base of the cone is a circle whose diameter is equal to the length of the edge of the cube.
∴ Radius of cone, r =15/2 cm
The height of the cone would be equal to the height of cube.
∴ Height of cone, h = 15 cm
Volume of the remaining portion = Volume of Cube − Volume of Cone
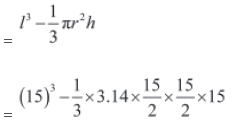
= 3375 − 883.125
= 2491.875 cm3
Thus, the volume of the remaining portion is 2491.875 cm3.
Example 2: A plastic toy is in the following shape. The diameter of the cylindrical shape is 7 cm, but the bottom of the toy has a hemispherical raised portion. The top of the toy is a cone of same base. If the height of the cylinder is 21 cm and cone is 4 cm, find the amount of air inside the toy. (Use π =22/7 )
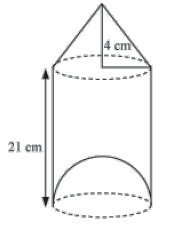
Solution:
Diameter of the cylinder = 7 cm
Radius of cylinder, r =7/2 cm
r =7/2 , is also the radius for cone and hemisphere.
Height of the cylinder, H = 21 cm
Height of the cone, h = 4 cm
∴ Volume of the toy = Volume of cylinder + Volume of Cone − Volume of Hemisphere
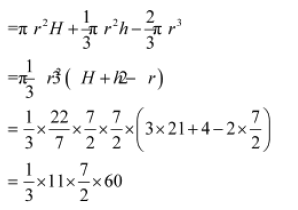
= 770 cm3
Thus, the volume of air inside the given toy is 770 cm3.
Example 3: A right triangle, whose perpendicular sides are 30 cm and 40 cm, is made to revolve about its hypotenuse. Find the volume of figure so obtained in terms of π.
Solution:
Let ABD be a right-angled triangle, such that AB = 30 cm and AD = 40 cm.
Using Pythagoras theorem, we have
BD2 = AB2 + AD2
BD2 =302+402=900+1600=2500
BD = √2500 =50 cm
After revolution, we have the following figure.
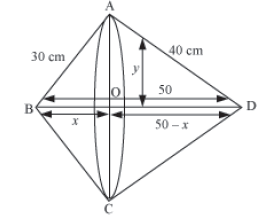
Let OB = x and OA = y
Using Pythagoras theorem in triangle AOB, we obtain
OA2 + OB2 = AB2
x2 + y2 = 302
y2 = 900 − x2 … (1)
Using Pythagoras theorem in triangle AOD, we obtain
OA2 + OD2 = AD2
y2 + (50 − x) 2 = 402
900 − x2 + 2500 + x2 − 100x = 1600 {using equation (1)}
100x = 1800
x = 18
On putting the value of x in equation (1), we obtain
y2 = 900 − x2 = 900 − 182 = 900 − 324 = 576
y = √576=24 cm
Here, y is the radius of the cones ABC and ADC.
Now, height of the cone ABC, x = 18 cm
Height of the cone ADC, 50 − x = 32 cm
Volume of the double cone = Volume of cone ABC + Volume of cone ADC
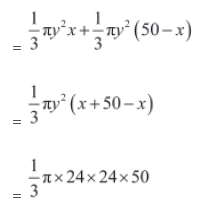
= 9600π cm3
Thus, the volume of the figure so obtained is 9600π cm3.
Example 4: An iron container is cylindrical in shape as shown in the figure. The inner and outer diameters are 12 cm and 14 cm respectively. The container has a solid base of width 1.5 cm and the total height of the container is 22.5 cm. If the mass of 1 cm3 of iron is 8 gm, find the weight of the container.
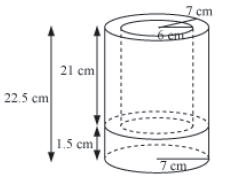
Solution:
The iron container consists of two cylinders.
1. A solid cylinder and
2. A hollow cylinder
External and internal diameters of the hollow cylinder are 14 and 12 cm respectively.
Hence, internal radius, r = 6 cm and external radius R = 7 cm
Height of the solid cylinder, h = 1.5 cm
∴ Height of the hollow cylinder, H = 22.5 − 1.5 = 21 cm
Volume of the iron used in the container = Volume of solid cylinder + Volume of hollow cylinder
= πR2h+π(R2 -r2)H
=22/7×7×7×1.5+22/7(72-62)×21
= 231 + 858
= 1089 cm3
Mass of 1 cm3 of iron = 8 gm
Mass of 1089 cm3 of iron = 1089 × 8 = 8712 gm = 8.712 kg
Thus, the weight of the container is 8.712 kg.
Conversion Of Solids From One Shape Into Another
In our daily life, we come across various shapes of objects. For example, we see the objects of wax (candle) in various shapes like cylindrical, conical, circular etc. Have you ever thought how these objects are made?
First of all, the wax is melted and after that the liquid wax is poured into containers which have the special shape in which we want to mould the wax. Then after cooling the wax we get the desired shape.
We also convert solids from one shape into another. For example, a metallic wire of cylindrical shape is melted and recast into a spherical shape; earth dug out from a well is uniformly distributed to form an embankment around it.
The main concept in such conditions is that the amount of material before the conversion remains the same as the amount of material after the conversion or we can say that the volume before the conversion and after the conversion remains constant.
Let us consider a situation where we have a ball which is made up of wax. We measured the radius of the ball and it came out to be 3 cm. Now, we want to make a candle of length 16
cm from the wax ball. What should be the radius of the mould so that no wax is wasted? We use this concept for solving the problems related to conversion of solids. Let us discuss
some examples based on the above idea.
Example 1: A solid right circular metallic cone of radius 10 cm and height 5 cm is melted and recast into a sphere. Find the radius of the sphere.
Solution:
Let us consider the above information geometrically.
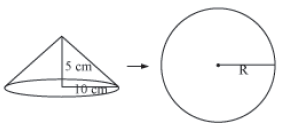
It is given that radius of cone, r = 10 cm
Height of cone, h = 5 cm
Let R be the radius of sphere.
Since the cone is melted to form a sphere,
Volume of metal before conversion = volume of metal after conversion
∴ Volume of cone = Volume of sphere
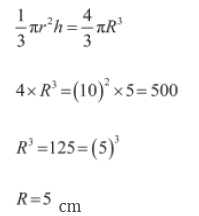
Thus, the radius of the sphere is 5 cm.
Example 2: If the volumes of a solid hemisphere, a solid right circular cone and a solid right circular cylinder of same base are equal, then find the ratio of their heights.
Solution:
Let us consider the above information by drawing figures.
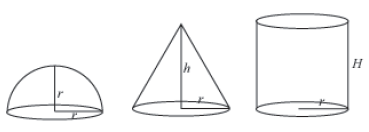
All the three solids have equal base, i.e. their radii are equal.
Let r be the radius of the above three figures. The height of the hemisphere will also be r.
Let the height of the cone and cylinder be h and H respectively.
But it is given that,
Volume of hemisphere = Volume of cone = Volume of cylinder
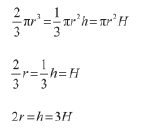
The LCM of 2, 1, and 3 is 6.
Now, let us write
2r=h=3H= 6x
⇒ 2r=6x,h=6x,3H=6x
Hence, r=3x,h=6x and H=2x
Now, r: h: H = 3x: 6x: 2x
r: h: H = 3: 6: 2
∴ Ratio of their heights = 3: 6: 2
Example 3: A solid right circular metallic cone of height 5 cm and radius 21 cm is melted to form some coins of diameter 2 cm and width 6 mm and some spherical balls of diameter 3 cm. If the ratio of the number of coins to the number of balls is 2:3, then find the number of coins and balls.
Solution:
For the cone,
Height, h = 5 cm and radius, r = 21 cm
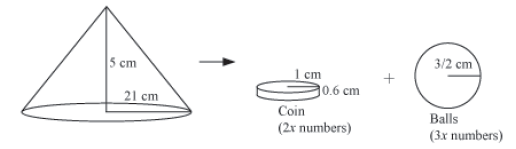
For cylindrical coin,
Diameter = 2 cm
So, radius, r1 = 1 cm
Height, h1 = 6 mm = 0.6 cm
For spherical balls,
Diameter = 3 cm
So, radius, r2 = 3/2 cm
Let number of spherical coins = 2x and number of spherical balls = 3x
Metallic cone is melted and recast to form coins and balls.
∴ Volume of coins + Volume of balls = Volume of Cone
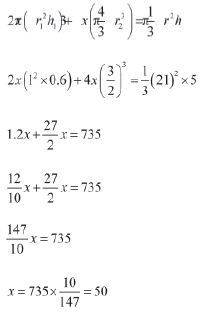
∴ Number of coins = 2x = 2 × 50 = 100
And number of spherical balls = 3x = 3 × 50 = 150
Example 4: A solid toy is in the form of a hemisphere surmounted by a right circular cone.The height of the cone is 10 cm and the diameter of the base is 14 cm. The toy is placed in a cylinder which is half filled with water. Find the height of increase in water level in the cylinder, if the radius of the cylinder is 14 cm.
Solution:
Let us draw the figure for the given information.
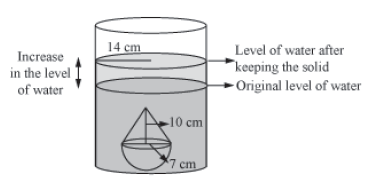
For the toy,
Diameter of the hemisphere = 14 cm
Radius of hemisphere, r = 7 cm (Also radius for cone)
Height of the cone, h = 10 cm
For the cylinder,
Radius, R = 14 cm
Let height of increase in the level of water = H When the toy is kept in the cylindrical vessel, the water will rise uniformly taking the shape of a cylinder, i.e. the increase in the level of water will be in the shape of a cylinder of radius 14 cm.
Volume of water raised in the cylinder = Volume of the toy
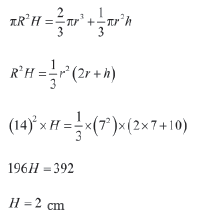
Thus, the water level will become 2 cm high after keeping the toy in the cylindrical vessel.
Surface Areas of Frustum of Cone
Look at the following figure.
In day to day life, we come across various shapes similar to this, such as a glass, a bucket, a funnel, etc. This shape is known as frustum of cone.
Now, can we describe what a frustum is?
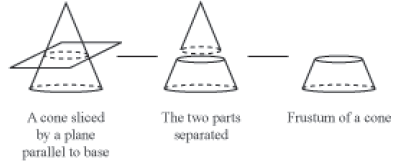
The solid obtained by cutting a cone by a plane parallel to its base is known as frustum of a cone.
We can observe from the following figure that a cone is sliced by a plane parallel to the base. After removing the smaller cone, we obtain a solid which is known as frustum of cone.
The given figure shows an iron tub and its dimensions. Its exterior curved surface is to be polished. Can we find the area of iron tub to be polished? [π=22/7]
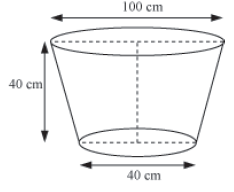
To find the total surface area of a frustum, we just need to add the areas of its two circular faces to its curved surfaces area.
Therefore,
Total surface area of frustum = Curved surface area + Area of two circular faces
Total surface area of a frustum = π(r1 + r2)l + πr12 + πr22
Let us look at some examples to understand the concept better.
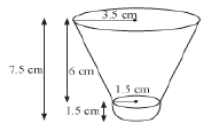
Example 1: A shuttle cock, which is used for playing badminton, has the shape of a frustum mounted on a hemisphere as shown in the following figure. The dimensions are also shown in the figure. Find the outer curved surface area of the shuttle cock. (Use π = 3.14)
Solution:
It is given that,
r1 = radius of upper end of frustum = 3.5 cm
r2 = radius of lower end of frustum = 1.5 cm (Also the radius of the hemisphere)
h = height of the frustum = 7.5-1.5=6 cm
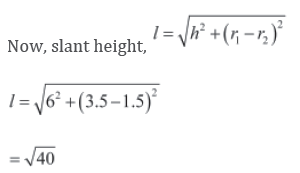
= 6.32 cm
Outer curved surface area of shuttle cock = C.S.A. of frustum + C.S.A. of hemisphere= 99.22 + 14.13
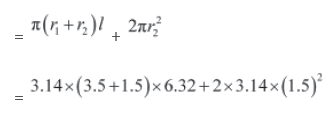
= 113.35 cm2
Thus, the required surface area is 113.35 cm2 .
Example 2: A solid is in the shape of the frustum of a cone. The radii of its circular ends are 7 cm and 14 cm. The total surface area of the solid is 2420 cm2. What is the height of the solid? [π=22/7]
Solution:
The solid is in the shape of a conical frustum with radii 7 cm and 14 cm and total surface area 2420 cm2.
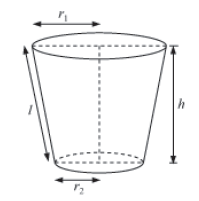
Let r1 and r2 be the radii of the solid. Let l and h be its slant height and height respectively.
The total surface area of the frustum is given by π=(r1+r2)l+πr12 +πr22 .
Here, r1 = 14 cm and r2 = 7 cm
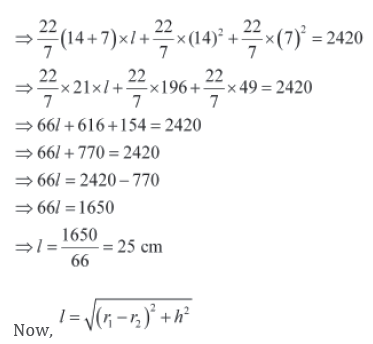
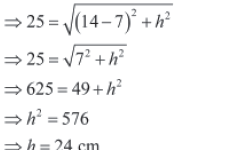
Thus, the height of the solid is 24 cm.
Example 3: The given figure shows a wooden shape which is in the shape of a frustum of a cone. The diameters of the upper and lower circular part are 4 ft and 8 ft respectively. Its curved surfaces are painted with red colour. If the cost of painting is Rs 660 at the rate of Rs 5 per ft2, then find the height of the wooden shape.
Solution:
The cost of painting is given to be Rs 660.
The area that was painted is the curved surface area of the wooden shape.
Also, it is given that the rate of painting is Rs 5 per ft2.
∴ C.S.A. of the wooden shape = 660/5 ft2= 132 ft2
We know, C.S.A. = π (r1 + r2) l, where r1 and r2 are the radii of the ends of the frustum shaped wood and l is the slant height.
r1=8/2=4 ft, r2=4/2 ft =2 ft
We have, π (r1 + r2) l = 132 ft2
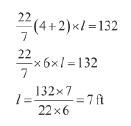
Let h be the height of the wooden shape.
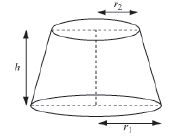
Then, we have
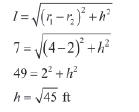
Thus, the height of the wooden shape is √45 ft.
Example 4: Adam brought a conical pancake (a cake eaten in USA) that was 16 cm high with vertical angle of 60° and kept it in a refrigerator. After sometime, his cousin Susan came and cut the pancake into two parts with the help of a knife at the middle point of its height and took the smaller part. She also covered the tissue paper entirely around the remaining cake. Calculate the least amount of paper in terms of π that she required to cover the pancake.
Solution:
Let us consider the following figure in order to understand the question properly.
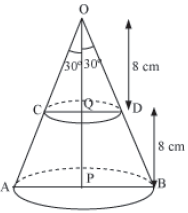
Adam brought the conical pancake OAB whose vertical angle ∠AOB = 60°.
Here, height of the pancake, OP = 16 cm
Let us consider Q as the mid-point of OP. Susan cut the pan cake into two parts through Q.
Therefore, we have OQ =16/2=8 cm
Also, ∠AOP and ∠COQ = 1/2×60° =30°
After cutting conical pancake OCD from pancake OAB, the remaining pancake is in the shape of a frustum.
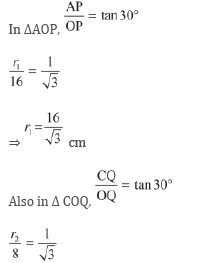

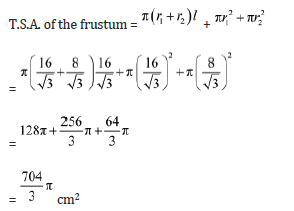
Thus, Susan required 704/3.π cm2 of paper to cover the remaining pancake.
Volume Of A Frustum Of A Cone
Suppose there is a container made up of metal sheet in the form of a frustum of a cone of height 14 cm with diameter of its lower and upper ends as 50 cm and 20 cm respectively.
Can we find the cost of honey which can completely fill the container at the rate of Rs 150 per litre?
Let us look at some more examples to understand the concept better.
Example 1: A metallic right circular cone, 14 cm high and whose vertical angle is 60°,is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter 7/6 mm, then find the length of the wire.
Solution:
Let us consider the following figure in order to understand the question properly.
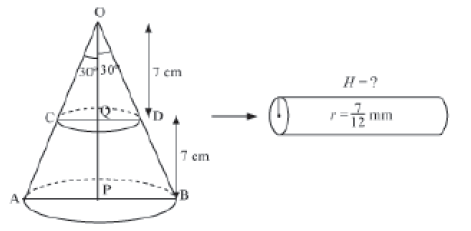
Let OAB be the cone whose vertical angle ∠AOB = 60°. Let r1 and r2 be the radii of the lower and upper end of the frustum.
Here, height of the cone, OP = 14 cm
Let us consider Q as the mid-point of OP.
After cutting the cone into two parts through Q,
OQ = 14/2=7 cm
Also, ∠AOP and ∠COQ = 1/2×60°=30°
After cutting cone OCD from cone OAB, the remaining solid obtained is a frustum.
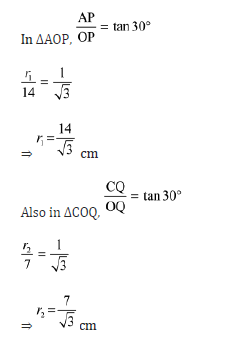
Height of the frustum, h = PQ = OP − OQ = 14 − 7 = 7 cm
For the cylinder shaped wire,
Radius, r =1/2×7/6 =7/12 mm = 7/120cm
Let the length of the wire be H.
It is given that the frustum is drawn into a cylindrical wire.
∴ Volume of Cylinder = Volume of Frustum
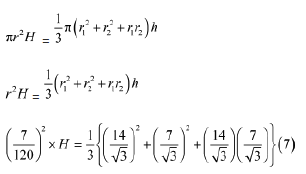
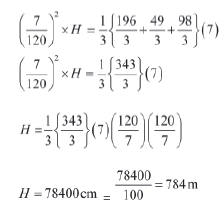
Thus, the length of the wire drawn from the frustum is 784 m.
Example 2: A hollow cone of height 30 cm is cut by a plane parallel to the base, and the upper portion is removed. If the volume of the remainder (frustum of cone) is 98/125 of the volume of the whole cone, then find the ratio of the altitudes of the frustum and the cone that is removed.
Solution:
Let us consider that cone OCD ( radius r2, height h2, and slant height l2) is removed from a cone OAB of radius r1, height h1, and slant height l1, where circular base CD is parallel to circular base AB.
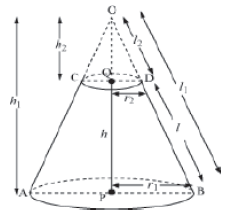
In the triangles OQD and OPB,
(i) ∠QOD = ∠POB
(ii) ∠ODQ = ∠OBP
(As base CD is parallel to base AB, corresponding angles are equal)
Hence, by AA Similarity Criterion,
ΔOQD ~ ΔOPB
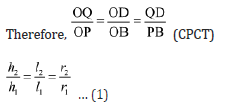
Given that volume of frustum = 98/125×volume of the whole cone
Volume of the cone OAB − Volume of cone OCD = 98/125×volume of cone OAB
Volume of cone OCD = 27/125 × volume of cone OAB

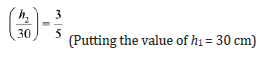
h2 = 18 cm
Now, PQ = h = h1-h2=30-18=12 cm
Hence, the section is made above 12 cm from the base.
Ratio of the altitudes of the frustum and the cone that is removed
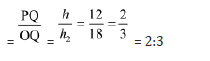

We hope the above Surface Area And Volume Class 10 Mathematics are useful for you. If you have any questions then post them in the comments section below. Our teachers will provide you an answer. Also refer to MCQ Questions for Class 10 Mathematics


